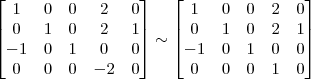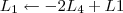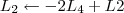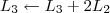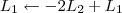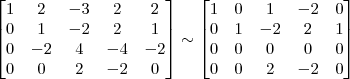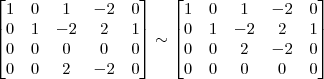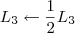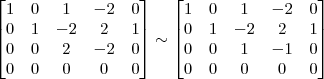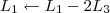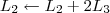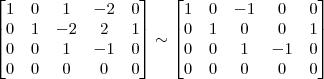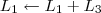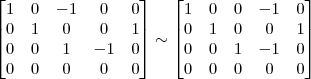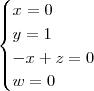Claudin escreveu:Eu resolvo do mesmo modo expresso no vídeo, transformando a diagonal principal em 1.
Mas você ainda está errando muitos passos no processo! Ao que parece, ainda lhe falta um pouco mais de atenção na hora de executar as operações.
Por exemplo, vamos analisar a última resolução que você enviou. Até o segundo passo, tudo está ok. O problema começa do terceiro passo em diante.
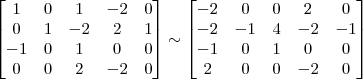
Vamos repetir o que você fez no segundo passo:
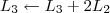
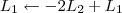
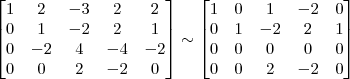
Devemos perceber duas coisas no final desse passo: 1) Os pivôs das linhas 1 e 2 já estão iguais a 1; 2) Para o próximo passo, é preciso transformar o pivô da linha 3 em 1.
Mas como você poderia transformar o pivô da linha 3 em 1, sem desfazer o trabalho que você já fez? Isto é, você tem que transformar esse pivô em 1, mas os termos da matriz que já são 0 devem continuar com esse valor.
A maneira mais simples nesse caso, seria trocar de lugar a linha 3 com a linha 4 e em seguida multiplicar a nova linha 3 por 1/2. Faríamos então os passos abaixo.
3º Passo)
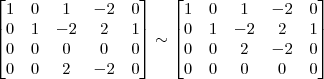 4º Passo)
4º Passo)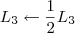
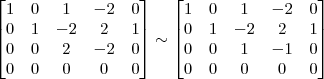
Devemos perceber duas coisas no final desse passo: 1) Não dá para transformar o pivô da linha 4 em 1 sem alterar os termos 0 que estão abaixo dos outros pivôs; 2) Para o próximo passo, precisamos transformar em 0 os termos acima dos pivôs.
5º Passo)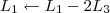
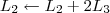
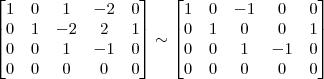
Devemos perceber duas coisas no final desse passo: 1) Não dá para transformar em 0 o termo -1 que está acima do pivô da linha 4; 2) Ainda há como transformar em 0 o termo -1 que está acima do pivô da linha 3.
6º Passo)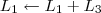
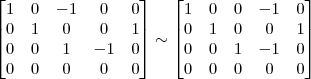
Devemos perceber uma coisa no final desse passo: 1) Não dá para transformar em 0 os termos -1 que estão acima do pivô da linha 4 sem alterar os outros termos da matriz que já são zero.
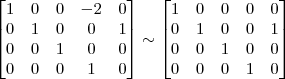
Com isso, o processo termina.
Note como no final obtemos a mesma matriz de minha primeira resolução.
ObservaçãoNas minhas últimas mensagens eu esqueci de responder a sua pergunta:
O sistema seria:
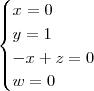
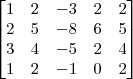

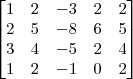


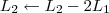
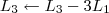
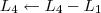
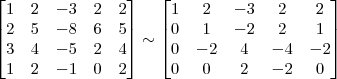
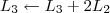
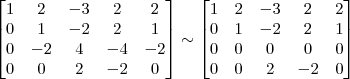

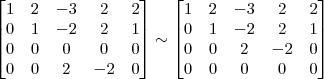
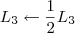
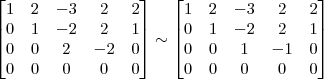
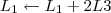
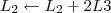
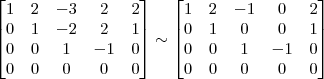
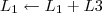
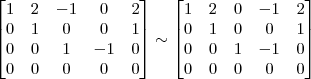
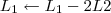
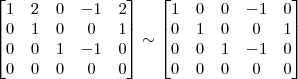
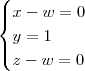

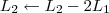
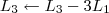
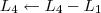
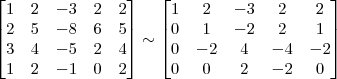
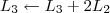
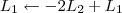
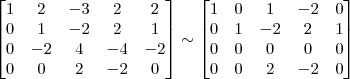
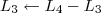
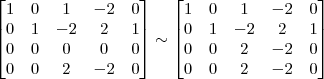
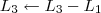
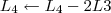
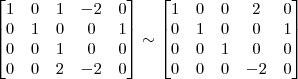
![L_4 \leftarrow [tex]\frac{-1}{2} L_4 \leftarrow [tex]\frac{-1}{2}](/latexrender/pictures/417e99a3e15d46f8753d7bb20712fc2a.png) L4[/tex]
L4[/tex]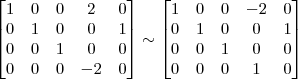
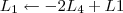
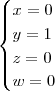

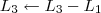 , o resultado correto seria:
, o resultado correto seria: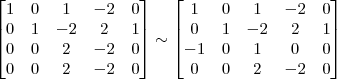

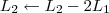
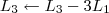
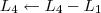
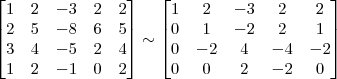
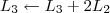
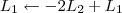
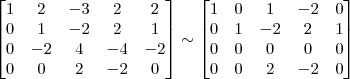
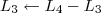
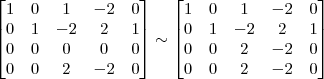
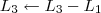
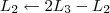
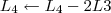
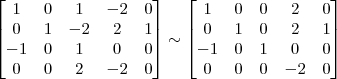
![L_4 \leftarrow [tex][tex]\frac{-1}{2}L4 L_4 \leftarrow [tex][tex]\frac{-1}{2}L4](/latexrender/pictures/59c6046357d4aab1eebeef8c0835c1e9.png)