"Se A é matriz quadrada de ordem 2 e
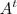sua transposta. Determinar A tal que 
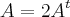."Tentei assumir valores para A e
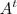, mas não deu muito certo...A forma que eu tentei foi a seguinte:
![A= \begin{pmatrix} a & b \\ c & d \end{pmatrix} \
A^t= \begin{pmatrix} a & c \\ b & d \end{pmatrix}
A= 2A^t \
A= \begin{pmatrix} 2a & 2c \\ 2b & 2d \end{pmatrix}
\begin{pmatrix} a & b \\ c & d \end{pmatrix} \ = \begin{pmatrix} 2a & 2c \\ 2b & 2d \end{pmatrix}
a = 2a \
b = 2c \
c= 2b \
d=2d \
--- \
a = 0 \
c = 2(2c) \Rightarrow c= 4c \Rightarrow c= 0 \
b= 2(0) \Rightarrow b = 0 \
d= 0](/latexrender/pictures/26af4dc0432173761e4660989d8361df.png "A= \begin{pmatrix} a & b \\ c & d \end{pmatrix} \
A^t= \begin{pmatrix} a & c \\ b & d \end{pmatrix}
A= 2A^t \
A= \begin{pmatrix} 2a & 2c \\ 2b & 2d \end{pmatrix}
\begin{pmatrix} a & b \\ c & d \end{pmatrix} \ = \begin{pmatrix} 2a & 2c \\ 2b & 2d \end{pmatrix}
a = 2a \
b = 2c \
c= 2b \
d=2d \
--- \
a = 0 \
c = 2(2c) \Rightarrow c= 4c \Rightarrow c= 0 \
b= 2(0) \Rightarrow b = 0 \
d= 0")
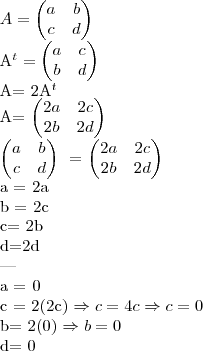
Sendo assim
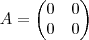
Gostaria de saber se é realmente assim que se faz.
por Alvadorn » Sáb Set 10, 2011 22:04
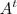sua transposta. Determinar A tal que 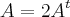."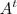, mas não deu muito certo...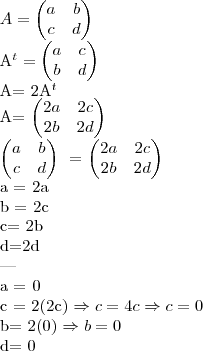
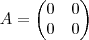
por MarceloFantini » Dom Set 11, 2011 19:55
Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante