 por Cleyson007 » Sáb Nov 01, 2008 00:51
por Cleyson007 » Sáb Nov 01, 2008 00:51
Olá, boa noite!!!
Não estou conseguindo resolver o seguinte exercício.... se alguém puder me ajudar agradeço de coração

, que Deus lhe abençoe!!!
A igualdade matricial
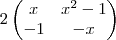
=
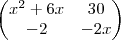
, com
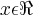
, é verdadeira, se e somente se:
a) -64
b) 64
c) 0
d) -64 ou 64
e) -64,0 ou 64
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Neperiano » Sáb Nov 01, 2008 11:14
por Neperiano » Sáb Nov 01, 2008 11:14
Ola
Essa questão se faz assim, voce primeiro multiplica o 2 pela primeira matriz, depois faça sistemas de equações envolvendo as duas matrizes.
Exemplo
2x=x+5
x+2+3
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Cleyson007 » Sex Mai 29, 2009 11:14
por Cleyson007 » Sex Mai 29, 2009 11:14
Olá, bom dia!
Resolvendo a equação matricial estou encontrando:
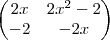
=
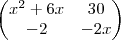
Resolvendo a igualdade das duas matrizes estou encontrando somente os valores para

:


.
Só que o enunciado pede o valor de

que torne verdadeira a igualdade, portanto,

.
Penso que a resolução está correta e o gabarito está errado

Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5157 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3604 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6003 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9695 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12811 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , que Deus lhe abençoe!!!
, que Deus lhe abençoe!!!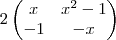 =
= 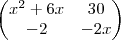 , com
, com 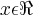 , é verdadeira, se e somente se:
, é verdadeira, se e somente se:
 , que Deus lhe abençoe!!!
, que Deus lhe abençoe!!!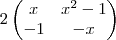 =
= 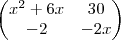 , com
, com 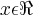 , é verdadeira, se e somente se:
, é verdadeira, se e somente se:

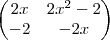 =
= 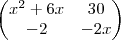
 :
: 
 .
. que torne verdadeira a igualdade, portanto,
que torne verdadeira a igualdade, portanto,  .
.
