 por Abner » Sex Abr 22, 2011 21:36
por Abner » Sex Abr 22, 2011 21:36
Considere um ponto no plano cartesiano dado pelo par ordenado P = (x, y) e vamos associar a esse ponto um vetor como sendo o segmento orientado que sai da origem (0, 0) até o ponto (x, y) e seja representado pela matriz coluna v=[x, y] . Seja uma matriz genérica A =[a b;c d] . Dizemos que a matriz A efetua uma transformação sobre o vetor v pela ação do produto.
1. Escreva o resultado do produto Av.
2. Mostre o resultado da transformação de A aos pontos (1, 0) e (0, 1)
3. Descreva em palavras, que tipo de transformação em pontos do plano a matriz A pode efetuar se c = 0 = b, a = 1 e d = 1. São quatro casos.
4. Descreva em palavras, que tipo de transformação em pontos do plano a matriz A pode efetuar se a = 0 = d, c = 1 e b =1 . São quatro casos.
Na item 1 fiz a multiplicação de linhas por colunas e obtive A=[ax+by;cx+dy] não sei se está certo....
Agora no item 2 estou em duvida se é para substituir a matriz A pelos pontos (1,0) e (0,1)???? e tb no item 3 e 4???se puderem me dar alguma explicação de como fazer agradeço....
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 23, 2011 09:23
por LuizAquino » Sáb Abr 23, 2011 09:23
1. Escreva o resultado do produto Av.
Se
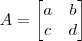
e
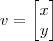
, então:
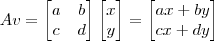
2. Mostre o resultado da transformação de A aos pontos (1, 0) e (0, 1)
Basta substituir x=1 e y=0 em
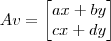
.
Faça o mesmo para x=0 e y=1.
3. Descreva em palavras, que tipo de transformação em pontos do plano a matriz A pode efetuar se c = 0 = b, a = 1 e d = 1. São quatro casos.
Lembre-se que se I é a matriz identidade, então Iv=v para qualquer v.
4. Descreva em palavras, que tipo de transformação em pontos do plano a matriz A pode efetuar se a = 0 = d, c = 1 e b =1 . São quatro casos.
Lembre-se que a reflexão do ponto (x, y) em relação a reta y=x é o ponto (y, x).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Abner » Sáb Abr 23, 2011 21:17
por Abner » Sáb Abr 23, 2011 21:17
No item 2 para x=1 e y=0
então ira ficar( a c )e para x=0 e y=1 ficara( b d)?
Mas não entendi no item 3 e 4 porque sao quatro casos...desde ja agradeço pela colaboração....
-
Abner
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Qua Jan 26, 2011 18:48
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 23, 2011 21:32
por LuizAquino » Sáb Abr 23, 2011 21:32
No item 2 para x=1 e y=0, então ira ficar( a c ) e para x=0 e y=1 ficara( b d)?
Apenas organizando com a notação correta:
(a) se x=1 e y=0, então
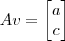
;
(b) se x=0 e y=1, então
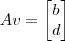
.
Mas não entendi no item 3 e 4 porque sao quatro casos...
Na minha opinião o texto dos itens 3 e 4 está mal colocado, haja vista que fixando os valores como foi informado haverá um tipo de transformação em cada caso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5165 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3605 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6004 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9698 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12817 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


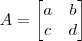 e
e 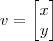 , então:
, então: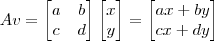
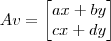 .
.
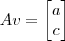 ;
;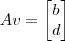 .
.