Mas preciso de uma ajuda para entender melhor este conteudo. E quando for para descobrir a lei de definição for matirzes como neste exemplo?
T:

tal que T
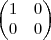 = (2,0,5) , T
= (2,0,5) , T  =(0,-1,3), T
=(0,-1,3), T  =(3,0,0) e T
=(3,0,0) e T  =(1,0,-2)
=(1,0,-2)Aguardo ajuda e obrigada!
Como faço para calcular a lei de definição de T, nesse caso?


 forma uma base para o domínio da transformação linear, nesse caso,
forma uma base para o domínio da transformação linear, nesse caso,  . É o caso desse exercício.
. É o caso desse exercício.

 ,
,  ,
,  e
e  .
.




 ,
,  ,
,  e
e  . Faça os cálculos e você verá que está tudo certo conforme os dados do exercício.
. Faça os cálculos e você verá que está tudo certo conforme os dados do exercício.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
