 por Priscylla Ramona » Sex Dez 17, 2010 10:54
por Priscylla Ramona » Sex Dez 17, 2010 10:54
Tenho q responder uma lista de exercicios de matrizes, mais so consegui responder uma questão e nem sei se esta certa.
As questões são as seguintes:
Dada a matriz quadrada
1
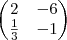
, Seja x o produto dos elementos da diagonal principal e seja y prodruto dos elementos da diagonal secundaria. Calcule x-y .
Eu vou colocar aqui o jeito q eu estava tentando resolver:
x= 2 e -1
y=

e -6
x-y=
(2+ (-1))- (

+ (-6)
(1)-
não consegui sair daqui, se alguem puder me ajudar eu agradeço.
-
Priscylla Ramona
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Dez 17, 2010 10:30
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por dagoth » Sex Dez 17, 2010 11:18
por dagoth » Sex Dez 17, 2010 11:18
x é o PRODUTO dos elementos da diagonal principal.
y é o PRODUTO dos elemenyos da diagonal secundaria.
logo, x = 2 * - 1 = -2
y = 1/3 * - 6 = -2
x - y = -2 - (-2) = -2 + 2 = 0.
-
dagoth
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Dez 16, 2010 21:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciência da Computação
- Andamento: cursando
 por Priscylla Ramona » Sex Dez 17, 2010 11:33
por Priscylla Ramona » Sex Dez 17, 2010 11:33
Muito obrigada!
me ajudou muito.
-
Priscylla Ramona
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Dez 17, 2010 10:30
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Priscylla Ramona » Sex Dez 17, 2010 13:26
por Priscylla Ramona » Sex Dez 17, 2010 13:26
respondi essa matriz e não sei se tah certa.
Dado A=
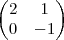
B=
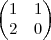
C=
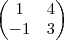
Determine 2A-C+2(A+B-C)
2
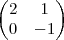
-
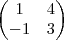
+2
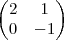
+
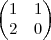
-
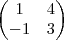
2
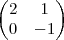
-
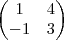
+2
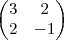
-
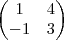
2
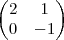
-
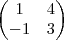
+2
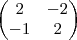
2
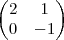
-
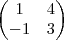
+2
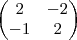
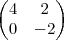
-
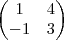
+
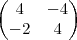
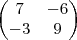
Se puderem me dizer se esta certo eu agradeço.
-
Priscylla Ramona
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Dez 17, 2010 10:30
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por dagoth » Sex Dez 17, 2010 14:10
por dagoth » Sex Dez 17, 2010 14:10
esta errada.

resulta em
2 -2
3 -4
-
dagoth
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Dez 16, 2010 21:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciência da Computação
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7173 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3576 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6730 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4705 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4816 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
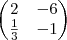
 e -6
e -6 + (-6)
+ (-6)

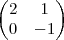
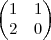
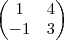
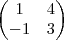 +2
+2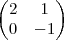 +
+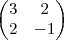 -
-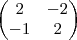
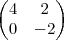 -
-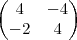
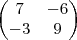

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
