 por DanielRJ » Sex Set 10, 2010 22:00
por DanielRJ » Sex Set 10, 2010 22:00
Olá pessoal como não tenho professor para corrigir e não tive oportunidade no chat trago então essa questão aqui mas para tirar duvida em calculos ok? minha resposta foi Zero então gostaria de saber se está correta.
Se
a é um numero real positivo e
n um inteiro qualquer o determinante da matriz
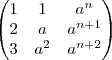
é:
a) não existe
b) zero
c)
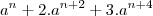
d)
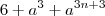
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Douglasm » Sex Set 10, 2010 23:15
por Douglasm » Sex Set 10, 2010 23:15
Filas proporcionais -> det = 0
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Set 11, 2010 22:11
por Molina » Sáb Set 11, 2010 22:11
danielcdd escreveu:Douglasm escreveu:Filas proporcionais -> det = 0
Bom valeu consegui enxergar. a segunda coluna está sendo multiplicada por
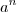
.
Bom tenho uma duvida basica aqui e vou postar aqui mesmo para não ficar criando topico.

denota o det da matriz A
A=
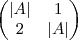
então os vaores de

são:
bom estou com uma duvida cruel qto o exercicio. minha duvida é tiro logo do modulo ou classifico assim: 
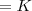 e acho as raizes e elimino a raiz negativa?
e acho as raizes e elimino a raiz negativa?
.

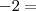


-

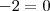
Boa noite.
O que você pode fazer, como você mesmo sugeriu é chamar
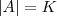
, Assim chegaríamos em:
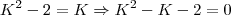
onde as raízes são
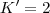
e
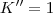
Mas esta não é a resposta, já que queremos achar os valores relacionados ao módulo de A. Então voltamos ao argumento
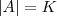
e substituímos os K's:
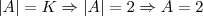
e



Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DanielRJ » Sáb Set 11, 2010 22:20
por DanielRJ » Sáb Set 11, 2010 22:20
molina escreveu:danielcdd escreveu:Douglasm escreveu:Filas proporcionais -> det = 0
Bom valeu consegui enxergar. a segunda coluna está sendo multiplicada por
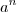
.
Bom tenho uma duvida basica aqui e vou postar aqui mesmo para não ficar criando topico.

denota o det da matriz A
A=
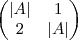
então os vaores de

são:
bom estou com uma duvida cruel qto o exercicio. minha duvida é tiro logo do modulo ou classifico assim: 
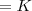 e acho as raizes e elimino a raiz negativa?
e acho as raizes e elimino a raiz negativa?
.

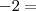


-

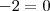
Boa noite.
O que você pode fazer, como você mesmo sugeriu é chamar
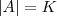
, Assim chegaríamos em:
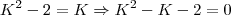
onde as raízes são
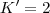
e
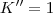
Mas esta não é a resposta, já que queremos achar os valores relacionados ao módulo de A. Então voltamos ao argumento
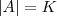
e substituímos os K's:
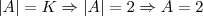
e



Opa molina valeu ai pela resposta mas é o seguinte acho que o exercicio não está considerando o
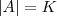
como modulo e sim como uma expressão qualquer. as respostas não batem. se fizermos considerando uma expressão qualquer, as raizes serão -1 e 2. e as raizes que postou acima foi o que eu encontrei , mas não tem essa opção!
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Dom Set 12, 2010 17:18
por MarceloFantini » Dom Set 12, 2010 17:18
Acredito então que a notação foi pessimamente usada, dando a impressão de que é módulo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinante
por Jessi » Seg Abr 20, 2009 16:10
- 1 Respostas
- 3188 Exibições
- Última mensagem por Molina

Seg Abr 20, 2009 17:04
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Sáb Set 11, 2010 18:47
- 4 Respostas
- 4681 Exibições
- Última mensagem por DanielRJ

Dom Set 12, 2010 12:56
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Dom Set 12, 2010 15:54
- 3 Respostas
- 3972 Exibições
- Última mensagem por MarceloFantini

Seg Set 13, 2010 00:03
Matrizes e Determinantes
-
- (ITA) DETERMINANTE
por natanskt » Sáb Nov 20, 2010 10:26
- 4 Respostas
- 4299 Exibições
- Última mensagem por vitall

Ter Jan 04, 2011 02:42
Matrizes e Determinantes
-
- (AFA) DETERMINANTE
por natanskt » Sáb Nov 20, 2010 10:46
- 3 Respostas
- 2837 Exibições
- Última mensagem por monicadiasf

Sex Abr 20, 2012 16:00
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
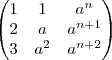 é:
é: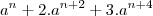
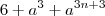

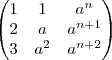 é:
é: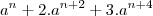
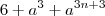


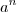 .
. denota o det da matriz A
denota o det da matriz A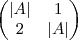 então os vaores de
então os vaores de  são:
são:
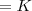 e acho as raizes e elimino a raiz negativa?
e acho as raizes e elimino a raiz negativa? .
.
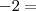

 -
-
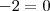

.
denota o det da matriz A
então os vaores de
são:
e acho as raizes e elimino a raiz negativa?
.
-
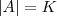 , Assim chegaríamos em:
, Assim chegaríamos em: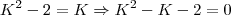
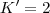 e
e 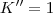
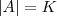 e substituímos os K's:
e substituímos os K's: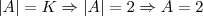 e
e 



.
denota o det da matriz A
então os vaores de
são:
e acho as raizes e elimino a raiz negativa?
.
-
, Assim chegaríamos em:
e
e substituímos os K's:
e
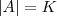 como modulo e sim como uma expressão qualquer. as respostas não batem. se fizermos considerando uma expressão qualquer, as raizes serão -1 e 2. e as raizes que postou acima foi o que eu encontrei , mas não tem essa opção!
como modulo e sim como uma expressão qualquer. as respostas não batem. se fizermos considerando uma expressão qualquer, as raizes serão -1 e 2. e as raizes que postou acima foi o que eu encontrei , mas não tem essa opção!


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)