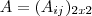 onde
onde 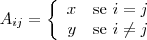 tais que
tais que  .
.a)0
b)1
c)2
d)3
e)4
gostaria de saber como se faz essa questão.. porque não entendi o enunciado. eu calculo a inversa depois fico sem saber o que fazer.

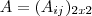 onde
onde 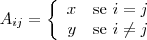 tais que
tais que  .
.
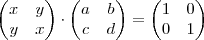
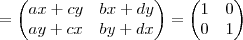
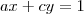
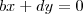
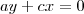
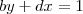
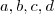 em função de
em função de  e
e  e depois iguale a matriz inicial à inversa. Feito isso, analise as possibilidades.
e depois iguale a matriz inicial à inversa. Feito isso, analise as possibilidades.

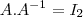 , até ai tudo bem mas porque a, b, c , d como variaveis? eu podia tentar criar uma inversa da matriz A tipo.. com as variaveis x e y?
, até ai tudo bem mas porque a, b, c , d como variaveis? eu podia tentar criar uma inversa da matriz A tipo.. com as variaveis x e y?



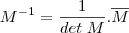
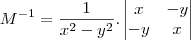
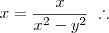
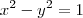
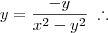


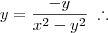
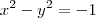
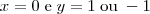

Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.