Alguem sabe a resposta dessas 2 fotos ai
pra segunda feira o mais rapido possível galera plz




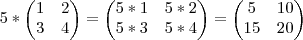
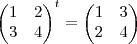
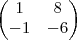

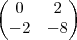


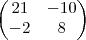


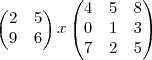 NAO pode ,pois a primeira tem 2 colunas e a segunda tem 3 linhas
NAO pode ,pois a primeira tem 2 colunas e a segunda tem 3 linhas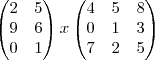 NAO pode, pois a primeira tem 2 colunas e a segunda tem tres linhas.
NAO pode, pois a primeira tem 2 colunas e a segunda tem tres linhas.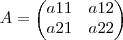
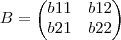
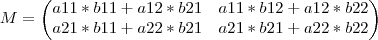
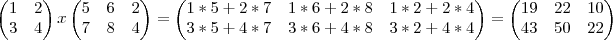

como e o nome desse assunto do matriz x matriz? e esse mesmo? tem como me passa um video tutorial para que eu veja, porque eu posso estar vendo um tutorial errado se eu mesmo pesquisaGebe escreveu:Ok, vou tentar deixar mais detalhado. Vamos começar exemplificando melhor a questão da condição para a multiplicação.
Para que duas matrizes possam ser multiplicadas a primeira matriz deve ter o seu numero de colunas igual ao numero de linhas da outra. Vou dar dois exemplos de operações que NÃO podem ser realizadas:
ex1:NAO pode ,pois a primeira tem 2 colunas e a segunda tem 3 linhas
ex2.:NAO pode, pois a primeira tem 2 colunas e a segunda tem tres linhas.
Note com isso que a ordem da operação na multiplicação de matrizes é importante. No segundo exemplo se as matrizes tivessem trocado de lugar seria possivel de realizar a multiplicação, pois teriamos a primeira matriz com 3 colunas e a segunda com 3 linhas.
Agora para a multiplicação de fato, vamos considerar duas matrizes genericas uma A e outra B (matrizes abaixo). Perceba que as matrizes tem 4 elementos: a11, a12, a21 e a22 e b11, b12, b21 e b22. Estes indices como mostrado abaixo representam a linha e a coluna do elemento.
Dizemos que a multiplicação é feita linha por coluna, pois os elementos da matriz resultante serão calculados multiplicando a linha da primeira matriz pela coluna da segunda. Como neste caso explicar apenas com palavras fica dificil, vamos fazer o exemplo com essas genericas, sendo M a matriz resultante de AxB e m (minusculo) os elementos de M.
m11, elemento da linha1 e coluna 1 da matriz resultante é calculado pela multiplicação da linha1 da matriz A pela coluna 1 da matriz B, portanto:
m11 = a11*b11 + a12*b21
m12, elemento da linha1 e coluna 2 da matriz resultante é calculado pela multiplicação da linha1 da matriz A pela coluna 2 da matriz B, portanto:
m12 = a11*b12 + a12*b22
m21, elemento da linha2 e coluna 1 da matriz resultante é calculado pela multiplicação da linha2 da matriz A pela coluna 1 da matriz B, portanto:
m21 = a21*b11 + a22*b21
m22, elemento da linha2 e coluna 2 da matriz resultante é calculado pela multiplicação da linha2 da matriz A pela coluna 2 da matriz B, portanto:
m22 = a21*b21 + a22*b22
Outro exemplo com numeros agora e diferentes dimensões:
Por fim vale notar outro ponto interessante, a matriz resultante da multiplicação terá o mesmo numero de linhas da primeira e numero de colunas igual a da segunda.
Espero ter ajudado, se as duvidas continuarem ou se puder especificar qual ponto te causa mais confusão, volte a perguntar. Bons estudos.


Gebe escreveu:Achei esse aqui https://www.youtube.com/watch?v=oYVBWG0wkoc
Eventualmente o youtube pode te sugerir videos semelhantes/relacionados caso tu não goste desse.
Há também um canal focado em ensino muito bom e didatico, o nome é MeSalva (youtube). Não procurei este assunto la, mas provavelmente deve ter tambem.

Gebe escreveu:Achei esse aqui https://www.youtube.com/watch?v=oYVBWG0wkoc
Eventualmente o youtube pode te sugerir videos semelhantes/relacionados caso tu não goste desse.
Há também um canal focado em ensino muito bom e didatico, o nome é MeSalva (youtube). Não procurei este assunto la, mas provavelmente deve ter tambem.

Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.