-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480812 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 543059 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506779 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 737045 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2184742 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por anselmojr97 » Seg Ago 15, 2016 22:33
por anselmojr97 » Seg Ago 15, 2016 22:33
Olá, pessoal. Estou respondendo umas questões sobre
matrizes, para dá uma revisada no assunto. Me deparei com essa questão, mas não consegui resolvê-la.
Peço a ajuda de vocês, se possível.
Eis a questão:
"Calcular todas as matrizex X, quadradas de ordem 2, tais que:
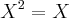
."
Desde já agradeço!
" Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim) "
-
anselmojr97
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 17, 2015 21:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por danielneiva » Ter Ago 16, 2016 23:03
por danielneiva » Ter Ago 16, 2016 23:03
Não entendi muito bem o que a questão pede... Mas os únicos números que cabem em x²=x são 0 e 1.
-
danielneiva
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Ago 16, 2016 22:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por anselmojr97 » Qua Ago 17, 2016 22:44
por anselmojr97 » Qua Ago 17, 2016 22:44
Oi, danielneiva. Nesse caso a resposta não é com números, mas sim com matrizes. Acho que tem usar matrizes genéricas ou coisa do tipo. Mas não sei como desenvolver. Mas obrigado por a resposta. Valeu!
" Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim) "
-
anselmojr97
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 17, 2015 21:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por adauto martins » Sex Ago 19, 2016 11:10
por adauto martins » Sex Ago 19, 2016 11:10
a
matriz 
deve ser quadrada e inversivel,o q. nao foi dado no enunciado,logo:

...logo o espaço-soluçao sera:

{

}...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 4596 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3230 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 5429 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9268 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12025 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
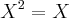 ."
."
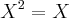 ."
."


 deve ser quadrada e inversivel,o q. nao foi dado no enunciado,logo:
deve ser quadrada e inversivel,o q. nao foi dado no enunciado,logo: ...logo o espaço-soluçao sera:
...logo o espaço-soluçao sera: {
{ }...
}...
