-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478701 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534717 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498306 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714029 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2136187 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por mota_16 » Sex Dez 06, 2013 11:12
por mota_16 » Sex Dez 06, 2013 11:12
Pessoal, não consigo resolver essa questão.
As
matrizes A, I e J são quadradas de ordem 2 e I é a
matriz identidade. Se a
matriz A =
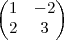
satisfaz as relações
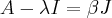
e
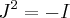
, com

e

números reais, então a
matriz J é igual a:
Resposta:
![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 07, 2013 11:45
por e8group » Sáb Dez 07, 2013 11:45
Uma forma é estabelecer uma relação entre os escaleres

com os termos da
matriz inversa de

.Nota a
matriz 
tem determinante não nulo e assim ela possui inversa e esta
matriz denotada por

é única .
Se
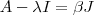
então
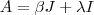
(1) .Multiplicando-se (1) por
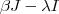
e usando
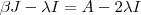
no lado esquerdo da igualdade e
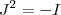
no lado direito ,obtemos
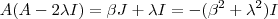
(2) . Logo ,
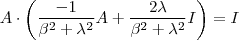
e assim concluímos que

(3) .
Agora tente concluir a parti daí .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sáb Dez 07, 2013 19:04
por mota_16 » Sáb Dez 07, 2013 19:04
Olá Santhiago,
Eu consegui entender as passagens, porém ao obter a
matriz inversa relacionadas com os escalares eu não tenho mais quem quero descobrir que é exatamente a
matriz J. Por isso, não consegui enxergar como a
matriz inversa vai me ajudar na resolução do problema. Pensei em fazer
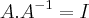
para descobrir os escalares. Como
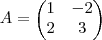
,
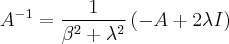
e
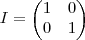
, teríamos:
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/501f688f5cc5d82b82842ada85d5b873.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/198b718a00ea39b73341b677c16fdf46.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/d48f64f33893203438310a00d4527205.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/f970343077885c2f6d6865686bf7bda9.png)
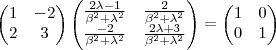
Resolvendo o produto:
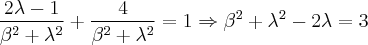
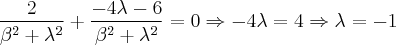
Substituindo na equação anterior, obtém-se
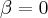
Acho que errei em algum lugar... É esse o raciocínio?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 07, 2013 20:33
por e8group » Sáb Dez 07, 2013 20:33
Parece que você obteve resultado errado devido erros de cálculos . Na verdade sugerir trabalhar com a
matriz inversa, por que tem um resultado para
matrizes 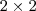
não singulares que nos fornece esta
matriz através da aplicação de uma fórmula . (veja :
http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) .
Comentário sobre sua resolução :
Na primeira linha após "teríamos " , aquela expressão é equivalente a de baixo
![A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I](/latexrender/pictures/cbc041bc731d574b16f6772bc0ba5e08.png)
que pode ser desenvolvida da seguinte forma :
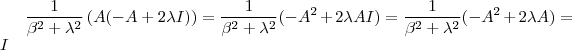
.
Ou ainda ,multiplicando ambos os lados da igualdade por
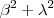
vamos obter
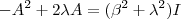
. Como
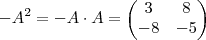
,
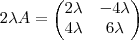
e
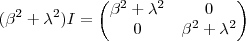
,segue
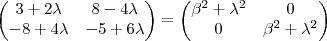
.
Daí , para que esta
matrizes sejam iguais teremos
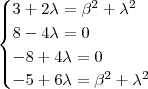
.
De acordo com segunda e terceira equação deste sistema temos
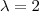
e assim o sistema se reduz a
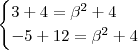
que nos dá
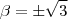
como solução .
Lembrando que
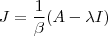
,substituindo os escalares pelos valores encontrados obterá a reposta .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sáb Dez 07, 2013 21:00
por mota_16 » Sáb Dez 07, 2013 21:00
santhiago muito obrigado pela ajuda! Entendi perfeitamente como fez! Vou rever meus cálculos e descobrir o erro.
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 07, 2013 21:32
por e8group » Sáb Dez 07, 2013 21:32
Há outra forma . Suponha
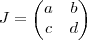
. Pelo que
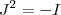
,segue

. Portanto
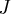
é invertível e sua inversa é
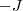
(*)
. Além disso,
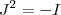
acarreta que
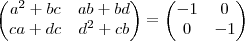
e assim
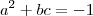
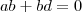
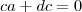
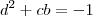
,
equivalentemente ,
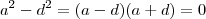
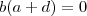
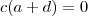
.
Analisando as soluções p/ primeira equação concluímos que
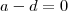
ou
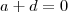
.Se ocorrer
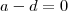
implicará
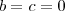
e
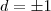
.Já na segunda possibilidade , temos

,para este caso devemos encontrar
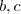
reais que cumpre
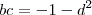
(**) e
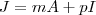
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :

. Logo ,
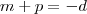
(1)
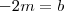
(2)
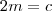
(3)
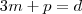
(4) ,
[(1) +(4)]
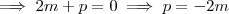
.
Então
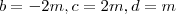
. Utilizando estes resultados em (**) ,
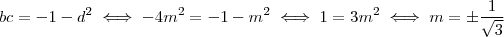
. E assim a,b,c,d estarão bem determinados .
Para aquele primeiro caso em que

,
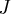
se exprimir por
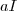
onde

é uma das possibilidades

ou

e assim teremos
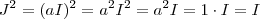
que contradiz o fato de
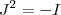
.
Editado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sex Dez 27, 2013 22:06
por mota_16 » Sex Dez 27, 2013 22:06
santhiago, tudo bem?
Estava estudando essa questão novamente e verifiquei que você postou uma nova resolução. E refazendo os passos eu não entendi o por quê do valor do d ser igual a um positivo ou um negativo em "Se ocorrer
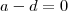
implicará
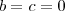
e
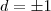
". Pode esclarecer?
santhiago escreveu:Há outra forma . Suponha
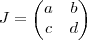
. Pelo que
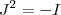
,segue

. Portanto
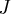
é invertível e sua inversa é
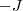
(*)
. Além disso,
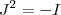
acarreta que
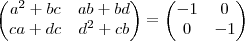
e assim
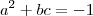
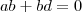
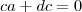
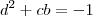
,
equivalentemente ,
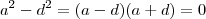
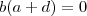
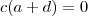
.
Analisando as soluções p/ primeira equação concluímos que
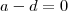
ou
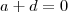
.Se ocorrer
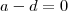
implicará
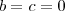
e
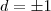
.Já na segunda possibilidade , temos

,para este caso devemos encontrar
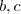
reais que cumpre
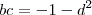
(**) e
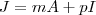
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :

. Logo ,
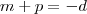
(1)
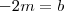
(2)
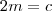
(3)
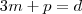
(4) ,
[(1) +(4)]
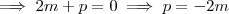
.
Então
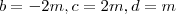
. Utilizando estes resultados em (**) ,
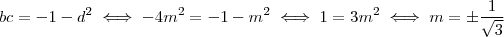
. E assim a,b,c,d estarão bem determinados .
Para aquele primeiro caso em que

,
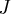
se exprimir por
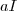
onde

é uma das possibilidades

ou

e assim teremos
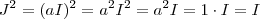
que contradiz o fato de
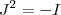
.
Editado .
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sex Dez 27, 2013 22:44
por e8group » Sex Dez 27, 2013 22:44
Boa noite . Vou rever a resposta [observei erroneamente a eq

,nesta época que respondi este tópico vi a mesma eq. como
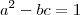
que em consequência nos
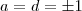
se
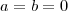
, a seguir vou rever minha resposta ].
Consegue ver que se
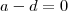
então
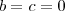
? Caso sim ,note que a
matriz 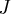
se escreve como
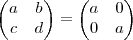
e deixando o número

em evidência ,temos que
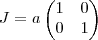
ou de forma mais compacta
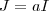
.Por hipótese a
matriz 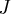
é tal que

.
Mas, se
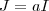
teremos
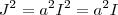
que é um absurdo , pois para qualquer número real

o seu quadrado será positivo e assim vemos que não existe

real p/ o qual
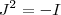
.
Outra forma de notares que

não é real é pela equação que já foi mencionada entre[]

.Com
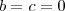
temos
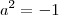
.
Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Sex Dez 27, 2013 23:07
por mota_16 » Sex Dez 27, 2013 23:07
Santhiago, perfeito nas explicações!
Entendi perfeitamente o que expôs! A única dúvida era mesmo no valor de d. Muito obrigado!
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por mota_16 » Sex Dez 27, 2013 23:45
por mota_16 » Sex Dez 27, 2013 23:45
Santhiago é possível enviar-lhe uma MP (mensagem particular) ? Tentei mas no meu cadastro não estou habilitado. Existe outra forma?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Sáb Dez 28, 2013 01:23
por e8group » Sáb Dez 28, 2013 01:23
Boa noite .Possuo o mesmo problema que você (não estou habilitado a enviar MP) .Suponho que somente os moderadores usufruem deste recurso . De qualquer forma, se precisar entrar em contato ,segue-se abaixo meu e-mail
guimaraes_thiago@live.com Att.,
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Identidade Trigonometrica
por MERLAYNE » Ter Abr 24, 2012 19:40
- 4 Respostas
- 2102 Exibições
- Última mensagem por DanielFerreira

Ter Abr 24, 2012 20:12
Trigonometria
-
- Função Identidade
por Jhenrique » Sáb Nov 17, 2012 19:29
- 0 Respostas
- 1162 Exibições
- Última mensagem por Jhenrique

Sáb Nov 17, 2012 19:29
Funções
-
- [Integral] Identidade
por klueger » Seg Mar 04, 2013 17:52
- 1 Respostas
- 1396 Exibições
- Última mensagem por young_jedi

Seg Mar 04, 2013 23:28
Cálculo: Limites, Derivadas e Integrais
-
- [Trigonometria] Identidade trigonometrica
por Alvadorn » Sáb Ago 13, 2011 17:47
- 2 Respostas
- 1567 Exibições
- Última mensagem por Alvadorn

Sáb Ago 13, 2011 20:27
Trigonometria
-
- identidade trigonométrica fundamental
por zenildo » Qui Jun 27, 2013 20:21
- 1 Respostas
- 1328 Exibições
- Última mensagem por young_jedi

Sex Jun 28, 2013 11:22
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
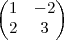 satisfaz as relações
satisfaz as relações 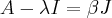 e
e 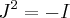 , com
, com  e
e  números reais, então a matriz J é igual a:
números reais, então a matriz J é igual a:![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)

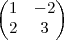 satisfaz as relações
satisfaz as relações 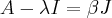 e
e 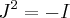 , com
, com  e
e  números reais, então a matriz J é igual a:
números reais, então a matriz J é igual a:![J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix} J=+ ou - \frac{1}{\sqrt[]{3}}
\begin{pmatrix}
-1 & -2 \\
2 & 1
\end{pmatrix}](/latexrender/pictures/c62514c673a86917f6b5e6e2ea624f7b.png)

 com os termos da matriz inversa de
com os termos da matriz inversa de  .Nota a matriz
.Nota a matriz  tem determinante não nulo e assim ela possui inversa e esta matriz denotada por
tem determinante não nulo e assim ela possui inversa e esta matriz denotada por  é única .
é única . 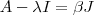 então
então 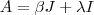 (1) .Multiplicando-se (1) por
(1) .Multiplicando-se (1) por 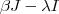 e usando
e usando 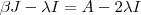 no lado esquerdo da igualdade e
no lado esquerdo da igualdade e 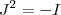 no lado direito ,obtemos
no lado direito ,obtemos 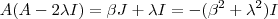 (2) . Logo ,
(2) . Logo , 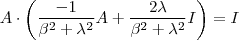 e assim concluímos que
e assim concluímos que  (3) .
(3) .
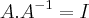 para descobrir os escalares. Como
para descobrir os escalares. Como 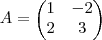 ,
, 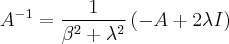 e
e 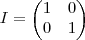 , teríamos:
, teríamos:![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-A + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/501f688f5cc5d82b82842ada85d5b873.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\left[ \frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(-
\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}
\right) + 2\lambda I \right) \right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/198b718a00ea39b73341b677c16fdf46.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}\left(
\begin{pmatrix}
-1 & 2 \\
-2 & -3
\end{pmatrix}
\right) +
\begin{pmatrix}
2\lambda & 0 \\
0 & 2\lambda
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/d48f64f33893203438310a00d4527205.png)
![\begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix} \begin{pmatrix}
1 & -2 \\
2 & 3
\end{pmatrix}\left[\frac{1}{{\beta}^{2}+{\lambda}^{2}}
\begin{pmatrix}
2\lambda-1 & 2 \\
-2 & 2\lambda+3
\end{pmatrix}
\right]=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}](/latexrender/pictures/f970343077885c2f6d6865686bf7bda9.png)
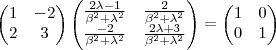
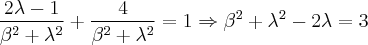
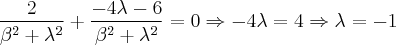
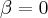

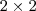 não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja : http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) .
não singulares que nos fornece esta matriz através da aplicação de uma fórmula . (veja : http://pt.wikipedia.org/wiki/Matriz_inv ... s_2.C3.972) . ![A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I A\left[ \frac{1}{\beta^2 + \lambda^2}(-A+ 2\lambda I) A\right] = I](/latexrender/pictures/cbc041bc731d574b16f6772bc0ba5e08.png) que pode ser desenvolvida da seguinte forma :
que pode ser desenvolvida da seguinte forma : 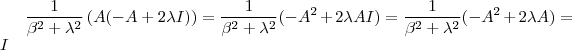 .
. 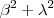 vamos obter
vamos obter 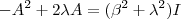 . Como
. Como 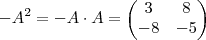 ,
, 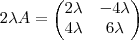 e
e 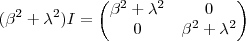 ,segue
,segue 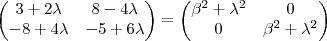 .
. 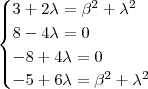 .
. 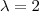 e assim o sistema se reduz a
e assim o sistema se reduz a 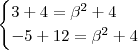 que nos dá
que nos dá 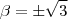 como solução .
como solução . 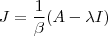 ,substituindo os escalares pelos valores encontrados obterá a reposta .
,substituindo os escalares pelos valores encontrados obterá a reposta .

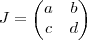 . Pelo que
. Pelo que 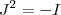 ,segue
,segue  . Portanto
. Portanto 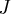 é invertível e sua inversa é
é invertível e sua inversa é 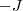 (*)
(*) 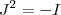 acarreta que
acarreta que 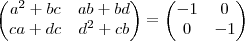 e assim
e assim 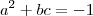
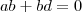
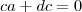
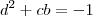 ,
,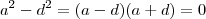
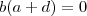
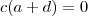 .
. 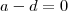 ou
ou 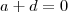 .Se ocorrer
.Se ocorrer 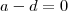 implicará
implicará 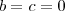 e
e 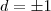 .Já na segunda possibilidade , temos
.Já na segunda possibilidade , temos  ,para este caso devemos encontrar
,para este caso devemos encontrar 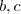 reais que cumpre
reais que cumpre 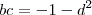 (**) e
(**) e 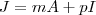 (Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :  . Logo ,
. Logo , 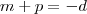 (1)
(1)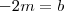 (2)
(2) 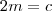 (3)
(3)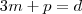 (4) ,
(4) , 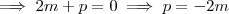 .
. 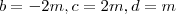 . Utilizando estes resultados em (**) ,
. Utilizando estes resultados em (**) , 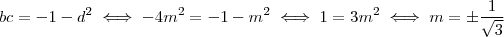 . E assim a,b,c,d estarão bem determinados .
. E assim a,b,c,d estarão bem determinados . ,
,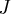 se exprimir por
se exprimir por 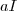 onde
onde  é uma das possibilidades
é uma das possibilidades  ou
ou  e assim teremos
e assim teremos 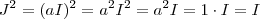 que contradiz o fato de
que contradiz o fato de 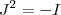 .
. 
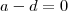 implicará
implicará 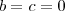 e
e 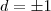 ". Pode esclarecer?
". Pode esclarecer?. Pelo que
,segue
. Portanto
é invertível e sua inversa é
(*)
acarreta que
e assim
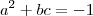
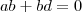
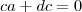
,
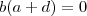
.
ou
.Se ocorrer
implicará
e
.Já na segunda possibilidade , temos
,para este caso devemos encontrar
reais que cumpre
(**) e
(Apenas dividi por \beta e definir os novos escalares como m e p ) . Prosseguindo :
. Logo ,
(1)
(2)
(3)
(4) ,
.
. Utilizando estes resultados em (**) ,
. E assim a,b,c,d estarão bem determinados .
,
se exprimir por
onde
é uma das possibilidades
ou
e assim teremos
que contradiz o fato de
.

 ,nesta época que respondi este tópico vi a mesma eq. como
,nesta época que respondi este tópico vi a mesma eq. como 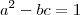 que em consequência nos
que em consequência nos 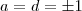 se
se 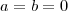 , a seguir vou rever minha resposta ].
, a seguir vou rever minha resposta ]. 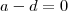 então
então 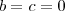 ? Caso sim ,note que a matriz
? Caso sim ,note que a matriz 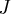 se escreve como
se escreve como 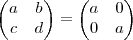 e deixando o número
e deixando o número  em evidência ,temos que
em evidência ,temos que 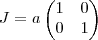 ou de forma mais compacta
ou de forma mais compacta 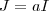 .Por hipótese a matriz
.Por hipótese a matriz 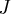 é tal que
é tal que  .
. 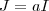 teremos
teremos 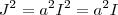 que é um absurdo , pois para qualquer número real
que é um absurdo , pois para qualquer número real  o seu quadrado será positivo e assim vemos que não existe
o seu quadrado será positivo e assim vemos que não existe  real p/ o qual
real p/ o qual 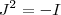 .
. não é real é pela equação que já foi mencionada entre[]
não é real é pela equação que já foi mencionada entre[]  .Com
.Com 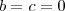 temos
temos 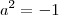 .
.





 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
