-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478662 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534429 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498018 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 713291 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2134827 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por DPassos » Ter Set 03, 2013 12:32
por DPassos » Ter Set 03, 2013 12:32
Estudei esse problema de determinante várias vezes pra ver se conseguia montar a matriz, porém não entendi os três tópicos que aparecem no enunciado, não entendi qual pode ser a região i e j, a questão de atribuição de valor 1 e 0, principalmente o zero, pois para mim todas as torres transmitem. E não entendi a lógica do último tópico quando diz que: uma torre não transmite sinal para ela mesma. Não posso nem falar muito das minhas tentativas de resolução, pois o máximo que entendi é que a matriz tem que ser quadrada - para encontrar determinante - Também gostaria de saber se o determinante encontrado tem que ser elevado ao quadrado?
O enunciado é o seguinte:
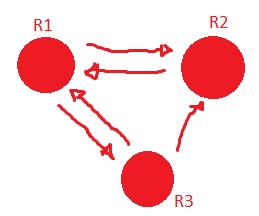
O esquema abaixo apresenta três torres repetidoras de telefonia celular que permitem a comunicação entre as regiões R1, R2 e R3. O sentido de cada seta indica que a torre de uma região transmite sinal para outra.
Seja A=(aij) a matriz que descreve as transmissões de sinais apresentadas no esquema, sendo que:
* aij=1 significa que há transmissão de sinal da torre repetidora da região i para torre repetidora da região j
* aij=0 significa que não há transmissão de sinal da torre repetidora da região i para a torre repetidora da região j
* Considere que uma torre repetidora não transmite sinal para ela mesma.
A partir dessas informações, o valor do determinante da matriz A^2 é:
Observação: caso a imagem da representação das torres na apareça no anexo que coloquei, fica aqui uma descrição da imagem: São três círculos (representação das torres), a disposição dos círculos forma um triângulo. Do círculo R1 sai um seta apontando para R2, do R1 uma apontando para o R3, do R3 uma apontando para R2, do R2 uma apontando para R1 e do R3 uma apontando para R1. a disposição dos círculos é esta:
R1 R2
R3
- Anexos
-
- Torres.jpg (13.26 KiB) Exibido 16235 vezes
-
DPassos
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Set 03, 2013 11:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: biologia
- Andamento: cursando
 por temujin » Ter Set 03, 2013 14:07
por temujin » Ter Set 03, 2013 14:07
Olá.
Uma matriz A=(aij) é um arranjo onde vc tem i linhas e j colunas. Monte sua matriz de modo que vc tenha como linhas R1, R2 e R3 e como colunas tb R1, R2 e R3:

O que o seu enunciado diz é que se a torre i transmite para a torre j, o valor de aij é 1. Se não transmite é 0. Ainda, nenhuma torre transmite para ela mesma, logo se i=j, então aij=0. Ou seja, na diagonal principal, Ri=Rj vc já sabe que terá 0 em cada entrada.
Agora, olhando para o seu desenho, vc vê que R3 transmite para R2, mas R2 não transmite para R3. Logo, vc terá que a23 = 0 e a32=1 ou que a23=1 e a32=0 (não importa qual, desde que aij=0 implique aji=1). Portanto, a sua matriz ficará:

Basta agora calcular o
determinante da matriz A. Como ele pede o det(A^2), lembre-se que pelo teorema de Binet det(AB)=det(A).det(B), portanto det(A^2)=det(A).det(A)
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por tatobonito » Dom Fev 28, 2016 22:44
por tatobonito » Dom Fev 28, 2016 22:44
.
-
tatobonito
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Fev 28, 2016 22:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informatica
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema envolvendo função
por marianacarvalhops » Sáb Mai 02, 2009 17:46
- 1 Respostas
- 4076 Exibições
- Última mensagem por Marcampucio

Sáb Mai 02, 2009 18:27
Funções
-
- Problema envolvendo equação
por ana tereza » Qui Set 10, 2009 23:47
- 3 Respostas
- 5337 Exibições
- Última mensagem por gabrielMAT

Qua Out 19, 2011 16:49
Sistemas de Equações
-
- Problema envolvendo capital
por Crist » Sex Mar 15, 2013 21:57
- 0 Respostas
- 1668 Exibições
- Última mensagem por Crist

Sex Mar 15, 2013 21:57
Equações Diferenciais Ordinárias e Aplicações
-
- Problema envolvendo função
por Carlos28 » Dom Abr 28, 2013 11:15
- 1 Respostas
- 1855 Exibições
- Última mensagem por young_jedi

Dom Abr 28, 2013 20:59
Funções
-
- Problema envolvendo derivadas.
por arthurvct » Sex Mai 03, 2013 20:16
- 4 Respostas
- 2547 Exibições
- Última mensagem por arthurvct

Qui Mai 16, 2013 19:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




