 por Colton » Sáb Out 02, 2010 20:22
por Colton » Sáb Out 02, 2010 20:22
+
+
Olá
Estou me debatendo já há mais de uma hora com a seguinte questão:
Calcule detQ, sabendo que Q é uma matriz 4 x 4 tal que detQ diferente de zero e Q^3+2Q^2 = 0.
Só consegui descobrir que se detQ = x, detQ^2 = x^2. detQ^3 = x^3...mas não consigo relacionar isto com a soma do cubo da matriz com o dobro do quadrado da matriz...
Há alguém aí que pode me dar uma orientação?
A resposta do livro é detQ = 16
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por Elcioschin » Seg Out 04, 2010 13:09
por Elcioschin » Seg Out 04, 2010 13:09
Vou tentar:
Q³ + 2*Q² = 0
(Q + 2)*Q² = 0
Como Q >< 0 -----> Q + 2 = 0 ----> Q = -2
Como a matriz é de ordem 4 ----> detQ = (-2)^4 -----> detQ = 16
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Colton » Seg Out 04, 2010 17:21
por Colton » Seg Out 04, 2010 17:21
+
+
Obrigado Elcioschin!
Às vezes o óbvio está aí e a gente não vê...
Abraços
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por Colton » Seg Out 04, 2010 17:40
por Colton » Seg Out 04, 2010 17:40
+
+
Olá Elcioschin... óia nóis aqui 'traveis!
Na verdade, eu também tinha chegado à conclusão que Q = -2...
O que eu não consegui visualisar é o significado disto, isto é o que quer dizer Q = -2 ???
É certo que elevando isto à quarta temos 16, mas aonde estamos pisando?
Abraço
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por MarceloFantini » Seg Out 04, 2010 18:45
por MarceloFantini » Seg Out 04, 2010 18:45
Acredito que a maneira seja essa:
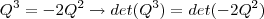
Pelas propriedades

, onde

é o tamanho da matriz, e

, temos:
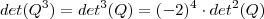
.
Como
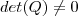
, podemos dividir por
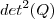
, finalizando:
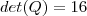
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Colton » Seg Out 04, 2010 19:59
por Colton » Seg Out 04, 2010 19:59
+
+
Olá Fantini
Eu acho que agora está certo.
Obrigado...é que estas propriedades (especialmente det(A^n) = det^n(A)) não consta do livro que eu venho estudando.
A outra propriedade consta, porém de maneira implícita...
Muito grato,
Abraço
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por MarceloFantini » Seg Out 04, 2010 20:23
por MarceloFantini » Seg Out 04, 2010 20:23
A propriedade

é uma consequência direta da propriedade

. Veja:
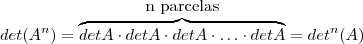
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Colton » Qua Out 06, 2010 11:31
por Colton » Qua Out 06, 2010 11:31
+
+
Olá Fantini,
Tomarei boa nota deste desenvolvimento. Grato.
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5163 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3604 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6004 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9696 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Giles » Qua Out 29, 2008 23:24
- 7 Respostas
- 12817 Exibições
- Última mensagem por Molina

Sex Nov 14, 2008 01:24
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



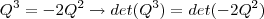
 , onde
, onde  é o tamanho da matriz, e
é o tamanho da matriz, e  , temos:
, temos: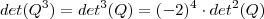 .
.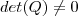 , podemos dividir por
, podemos dividir por 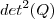 , finalizando:
, finalizando: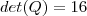


 é uma consequência direta da propriedade
é uma consequência direta da propriedade  . Veja:
. Veja: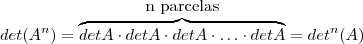
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.