Você obteve o sistema corretamente. Você precisa considerar ainda mais uma equação para resolver completamente o problema. Mas falemos dela depois. Atenhamo-nos agora a seguir os seus passos!
Note que subtraindo a primeira equação da última obtemos
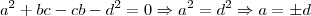
Mas, estudando a segunda e terceira equação não faz sentido
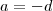
já que isso implicaria em
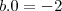
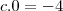
o que é um absurdo!
Portanto, nossa primeira constatação é que

.
Agora, se você dividir a segunda equação pela terceira encontrará uma relação linear entre

e

. Veja
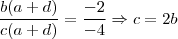
Substituindo essa informação na primeira equação temos que
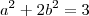
Ou seja, se
escolhermos(imaturamente)

como um parâmetro livre a solução do sistema é



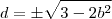
Uma exigência que deve ser feita é
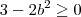
que implica em
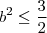
.
Agora, já que
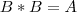
, então
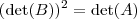
. Isto é,
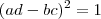
Mas, de acordo com nossa solução isto é
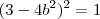
que nos dá as possibilidades
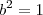
ou
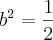
. Ambas estão de acordo com a exigência
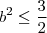
. Portando, existe mais de uma única matriz

tal que
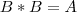
. As matrizes serão da forma
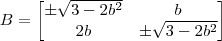
com
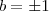
ou
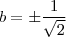
.
A matriz

conter elementos negativos
E positivos significa, instintivamente, que os elementos de

não podem ser, simultaneamente, todos positivos
ou todos negativos. Isto limita algumas escolhas de sinais na diagonal principal combinadas a escolha de

. Este fato se observa voltando a equação
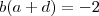
Se

, então
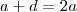
. Assim,
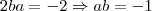
.
Portanto,

e

nunca podem ter o mesmo sinal! Se você escolher

ou
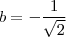
então terá, necessariamente, que selecionar as raízes positivas da diagonal principal de

. Caso contrário, as negativas. Eu acho que isto dá umas 4 possibilidades de matrizes

diferentes! E você queria apenas uma, hein? ;B kkk


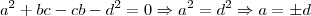
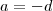 já que isso implicaria em
já que isso implicaria em 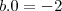
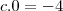
 .
. e
e  . Veja
. Veja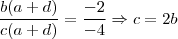
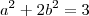



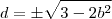
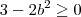 que implica em
que implica em 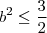 .
. 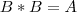 , então
, então 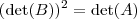 . Isto é,
. Isto é,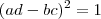
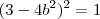
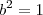 ou
ou 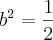 . Ambas estão de acordo com a exigência
. Ambas estão de acordo com a exigência  tal que
tal que 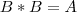 . As matrizes serão da forma
. As matrizes serão da forma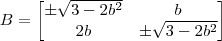
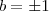 ou
ou 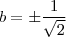 .
. conter elementos negativos
conter elementos negativos 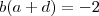
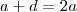 . Assim,
. Assim, 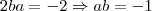 .
.  e
e  ou
ou 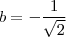 então terá, necessariamente, que selecionar as raízes positivas da diagonal principal de
então terá, necessariamente, que selecionar as raízes positivas da diagonal principal de 