 por rah_marques » Qua Out 21, 2009 18:08
por rah_marques » Qua Out 21, 2009 18:08
A questão é a seguinte:
Considere a matriz mostrada na figura a seguir:
A=
![\left[1\;\;\;\sqrt[]{-3} \right] \left[1\;\;\;\sqrt[]{-3} \right]](/latexrender/pictures/ef416b8bbba0f3d7b58f14dee252e72d.png)
![\left[ \sqrt[]{3}\;\;\;\;\;\, 1
\right] \left[ \sqrt[]{3}\;\;\;\;\;\, 1
\right]](/latexrender/pictures/c4fa74b48008c29303b82536181c7d01.png)
Determine
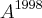
.
Eu tentei achar um padrão, então fui resolvendo
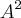
e
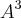
, subistituindo
![\sqrt[]{-3} \sqrt[]{-3}](/latexrender/pictures/6dbb163aa79a01894ca19d69c6ebbc04.png)
por i
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
e ficou assim:
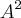
=
![\left[1 + 3i\;\;\;\; 2i\sqrt[]{3} \right] \left[1 + 3i\;\;\;\; 2i\sqrt[]{3} \right]](/latexrender/pictures/34f3c7e1fbc5696c2a124c7346921337.png)
![\left[2 \sqrt[]{3}\;\;\;\;\;\;1 + 3i \right\;\;\;] \left[2 \sqrt[]{3}\;\;\;\;\;\;1 + 3i \right\;\;\;]](/latexrender/pictures/5a22cd4a31e1604ab0437bc367c39325.png)
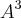
=
![\left[1 + 9i\;\;\;\; 3i\sqrt[]{3} + 3{i}^{2}\sqrt[]{3} \right] \left[1 + 9i\;\;\;\; 3i\sqrt[]{3} + 3{i}^{2}\sqrt[]{3} \right]](/latexrender/pictures/2ea1a943ed4e6dc1d5593315a1cb3902.png)
![\left[3\sqrt[]{3}+ 3i\sqrt[]{3}\;\;\;\;\;\;\;1+ 9i \right] \left[3\sqrt[]{3}+ 3i\sqrt[]{3}\;\;\;\;\;\;\;1+ 9i \right]](/latexrender/pictures/19a313c40c26736e408551b7693229d5.png)
Mas, não consegui sair daí.
Será que alguém pode me ajudar, por favor?
Obrigada
-
rah_marques
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Out 08, 2009 23:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UFES
por Guilherme Carvalho » Ter Mai 10, 2011 17:05
- 2 Respostas
- 2048 Exibições
- Última mensagem por Guilherme Carvalho

Qua Mai 11, 2011 12:04
Logaritmos
-
- Questão da UFES
por Ana29Carolina » Qui Mai 05, 2016 11:38
- 4 Respostas
- 4206 Exibições
- Última mensagem por Ana29Carolina

Seg Mai 09, 2016 17:32
Lógica
-
- Ajuda por favor.. Questão de prova HJ
por Erich » Qui Fev 24, 2011 11:58
- 3 Respostas
- 4144 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 03:34
Desafios Fáceis
-
- [Inequação Modular] Alguém por favor me ajuda nessa questão?
por FuturoFuturista » Ter Jan 22, 2013 21:27
- 1 Respostas
- 2647 Exibições
- Última mensagem por e8group

Ter Jan 22, 2013 22:15
Inequações
-
- Ajuda para resolver 4 questão de juros compostos por favor
por reuel » Qua Mar 20, 2013 00:58
- 1 Respostas
- 5962 Exibições
- Última mensagem por leticiaac

Seg Mar 02, 2015 17:20
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left[1\;\;\;\sqrt[]{-3} \right] \left[1\;\;\;\sqrt[]{-3} \right]](/latexrender/pictures/ef416b8bbba0f3d7b58f14dee252e72d.png)
![\left[ \sqrt[]{3}\;\;\;\;\;\, 1
\right] \left[ \sqrt[]{3}\;\;\;\;\;\, 1
\right]](/latexrender/pictures/c4fa74b48008c29303b82536181c7d01.png)
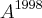 .
.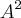 e
e 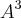 , subistituindo
, subistituindo ![\sqrt[]{-3} \sqrt[]{-3}](/latexrender/pictures/6dbb163aa79a01894ca19d69c6ebbc04.png) por i
por i![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) e ficou assim:
e ficou assim: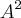 =
=![\left[1 + 3i\;\;\;\; 2i\sqrt[]{3} \right] \left[1 + 3i\;\;\;\; 2i\sqrt[]{3} \right]](/latexrender/pictures/34f3c7e1fbc5696c2a124c7346921337.png)
![\left[2 \sqrt[]{3}\;\;\;\;\;\;1 + 3i \right\;\;\;] \left[2 \sqrt[]{3}\;\;\;\;\;\;1 + 3i \right\;\;\;]](/latexrender/pictures/5a22cd4a31e1604ab0437bc367c39325.png)
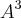 =
=![\left[1 + 9i\;\;\;\; 3i\sqrt[]{3} + 3{i}^{2}\sqrt[]{3} \right] \left[1 + 9i\;\;\;\; 3i\sqrt[]{3} + 3{i}^{2}\sqrt[]{3} \right]](/latexrender/pictures/2ea1a943ed4e6dc1d5593315a1cb3902.png)
![\left[3\sqrt[]{3}+ 3i\sqrt[]{3}\;\;\;\;\;\;\;1+ 9i \right] \left[3\sqrt[]{3}+ 3i\sqrt[]{3}\;\;\;\;\;\;\;1+ 9i \right]](/latexrender/pictures/19a313c40c26736e408551b7693229d5.png)

![\left[1\;\;\;\sqrt[]{-3} \right] \left[1\;\;\;\sqrt[]{-3} \right]](/latexrender/pictures/ef416b8bbba0f3d7b58f14dee252e72d.png)
![\left[ \sqrt[]{3}\;\;\;\;\;\, 1
\right] \left[ \sqrt[]{3}\;\;\;\;\;\, 1
\right]](/latexrender/pictures/c4fa74b48008c29303b82536181c7d01.png)
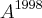 .
.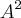 e
e 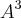 , subistituindo
, subistituindo ![\sqrt[]{-3} \sqrt[]{-3}](/latexrender/pictures/6dbb163aa79a01894ca19d69c6ebbc04.png) por i
por i![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) e ficou assim:
e ficou assim: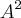 =
=![\left[1 + 3i\;\;\;\; 2i\sqrt[]{3} \right] \left[1 + 3i\;\;\;\; 2i\sqrt[]{3} \right]](/latexrender/pictures/34f3c7e1fbc5696c2a124c7346921337.png)
![\left[2 \sqrt[]{3}\;\;\;\;\;\;1 + 3i \right\;\;\;] \left[2 \sqrt[]{3}\;\;\;\;\;\;1 + 3i \right\;\;\;]](/latexrender/pictures/5a22cd4a31e1604ab0437bc367c39325.png)
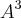 =
=![\left[1 + 9i\;\;\;\; 3i\sqrt[]{3} + 3{i}^{2}\sqrt[]{3} \right] \left[1 + 9i\;\;\;\; 3i\sqrt[]{3} + 3{i}^{2}\sqrt[]{3} \right]](/latexrender/pictures/2ea1a943ed4e6dc1d5593315a1cb3902.png)
![\left[3\sqrt[]{3}+ 3i\sqrt[]{3}\;\;\;\;\;\;\;1+ 9i \right] \left[3\sqrt[]{3}+ 3i\sqrt[]{3}\;\;\;\;\;\;\;1+ 9i \right]](/latexrender/pictures/19a313c40c26736e408551b7693229d5.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.