 por GABRIELA » Ter Set 01, 2009 17:57
por GABRIELA » Ter Set 01, 2009 17:57
PODERIA ME AJUDAR COMO FAÇO PARA RESOLVER EQUAÇÃO COM MATRIZES?
TENHO ESSE:
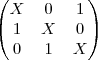
= 0
NÃO SEI NEM POR ONDE COMEÇA ESSA EQUAÇÃO.
-
GABRIELA
- Usuário Parceiro

-
- Mensagens: 73
- Registrado em: Seg Ago 31, 2009 17:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Ter Set 01, 2009 19:27
por Elcioschin » Ter Set 01, 2009 19:27
A sua dúvida é muito básica.
Vou resolver abaixo mas talvez você não entenda, pois não conhece a teoria.
Sugiro estudar "Matrizes - Determinantes- Regra de Sarrus"
X*X*X + 1*1*1 + 0*0*0 - 0*X*1 - 1*0*X - 1*0*X = 0
X³ + 1 = 0 -----> X³ = -1 ----> X = - 1
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação de Matrizes - Como Resolver
por juniocs » Qua Set 19, 2012 09:44
- 11 Respostas
- 6548 Exibições
- Última mensagem por Cleyson007

Qua Set 19, 2012 17:10
Álgebra Linear
-
- Como resolver equação diofantina utilizndo matrizes?
por joaofonseca » Qui Dez 13, 2012 17:25
- 2 Respostas
- 2960 Exibições
- Última mensagem por joaofonseca

Sex Dez 14, 2012 11:51
Teoria dos Números
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5165 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3605 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 6004 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
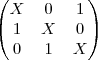

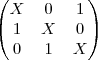





 .
.



