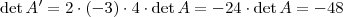por vanessafey » Sex Set 02, 2011 22:52
por vanessafey » Sex Set 02, 2011 22:52
Baixei uma apostila do cursinho da UFSC e não consigo resolver esta inversão de matrizes. O gabarito apresenta a resposta(-48) e eu sempre encontro 0.

- determinantes.png (4.89 KiB) Exibido 3755 vezes
Comecei da seguinte forma:
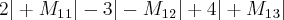
Editado pela última vez por
vanessafey em Sáb Set 03, 2011 00:21, em um total de 1 vez.
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Set 03, 2011 00:03
por MarceloFantini » Sáb Set 03, 2011 00:03
Vanessa, não entendo seu desenvolvimento. Pode explicar um pouco mais?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vanessafey » Sáb Set 03, 2011 00:12
por vanessafey » Sáb Set 03, 2011 00:12
Desculpe-me postei o anexo errado, lógico que fica incompreensível...

- determinantes.png (4.89 KiB) Exibido 3758 vezes
Tentei resolver por cofator relativo à primeira linha.
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessafey » Sáb Set 03, 2011 16:35
por vanessafey » Sáb Set 03, 2011 16:35
Muito obrigada! Nessas horas eu percebo como consigo complicar algo simples!
Vou continuar os exercícios...
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inversão
por admin » Sáb Jul 21, 2007 01:16
- 6 Respostas
- 6243 Exibições
- Última mensagem por Molina

Seg Jun 15, 2009 21:18
Desafios Médios
-
- Integral Dupla e inversao
 por ivoski » Ter Ago 14, 2012 18:12
por ivoski » Ter Ago 14, 2012 18:12
- 1 Respostas
- 2457 Exibições
- Última mensagem por LuizAquino

Qui Ago 23, 2012 18:32
Cálculo: Limites, Derivadas e Integrais
-
- [Cinemática] Inversão de movimento + grafico
por XxXMarlonXxX » Dom Out 07, 2012 02:16
- 3 Respostas
- 4462 Exibições
- Última mensagem por XxXMarlonXxX

Dom Out 07, 2012 15:53
Dúvidas Pendentes (aguardando novos colaboradores)
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5163 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3604 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
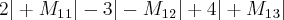

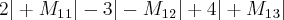





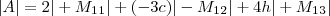
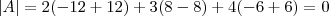

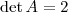 . Com a nova matriz A', temos que
. Com a nova matriz A', temos que