-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478727 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534982 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498572 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714833 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2137514 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por GrazielaSilva » Qui Out 04, 2012 12:42
por GrazielaSilva » Qui Out 04, 2012 12:42
Obter 3 números em PA de modo que sua soma seja 18 e seu produto 66.
-
GrazielaSilva
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Set 27, 2012 12:56
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Qui Out 04, 2012 13:35
por young_jedi » Qui Out 04, 2012 13:35
veja que uma PA tem os seguintes termos
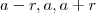
onde a é o termo central e r é a razão
somando os termos


dai voce tira o valor de a, depois aplicando o produto dos termos voce encontra a razão r.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por GrazielaSilva » Sex Out 05, 2012 01:22
por GrazielaSilva » Sex Out 05, 2012 01:22
Obrigada! Tentarei

-
GrazielaSilva
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Set 27, 2012 12:56
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.G. (Encontrar os termos)
por Rafael16 » Qua Jul 18, 2012 23:15
- 1 Respostas
- 2133 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 00:02
Progressões
-
- [ PA ] Encontrar termos
por GrazielaSilva » Qui Out 11, 2012 12:25
- 1 Respostas
- 1417 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 14:08
Progressões
-
- [Progressões] Encontrar os primeiros termos
por GrazielaSilva » Sex Set 28, 2012 11:28
- 2 Respostas
- 8433 Exibições
- Última mensagem por Yokotoyota

Qui Fev 04, 2016 03:09
Progressões
-
- Encontrar a1 em uma progressão de 3 termos com razão variáve
por parrala » Dom Out 04, 2015 19:13
- 3 Respostas
- 7299 Exibições
- Última mensagem por nakagumahissao

Seg Out 05, 2015 01:22
Progressões
-
- Termos da P.A e P.G.
por Cleyson007 » Dom Dez 27, 2009 11:18
- 2 Respostas
- 2033 Exibições
- Última mensagem por Cleyson007

Dom Dez 27, 2009 14:30
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



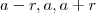






 , avisa que eu resolvo.
, avisa que eu resolvo.

