-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480408 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 540648 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 504487 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 730433 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2168808 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por andersontricordiano » Qua Abr 13, 2011 17:32
por andersontricordiano » Qua Abr 13, 2011 17:32
Qual é o valor de
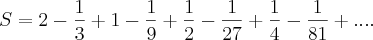
Detalhe a resposta é:

Mas eu fiz no meu calculo deu:
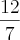 Por favor resolvem esse calculo!
Por favor resolvem esse calculo!
Agradeço quem resolver
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qua Abr 13, 2011 19:45
por FilipeCaceres » Qua Abr 13, 2011 19:45
Observe que podemos reescrever a equação da seguinte forma,
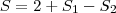
Onde
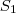
e
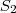
valem

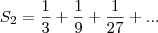
Como
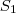
e
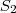
formam uma PG infinita, temos que

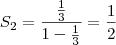
Portanto,
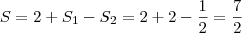
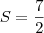
Espero que entenda.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Séries] Série convergente ou divergente?
por RafaelPereira » Ter Jun 18, 2013 13:31
- 2 Respostas
- 1971 Exibições
- Última mensagem por RafaelPereira

Ter Jun 18, 2013 17:49
Sequências
-
- SERIE CONVERGENTE DE NUMEROS COMPLEXOS
 por Jadiel Carlos » Sex Jan 19, 2018 02:35
por Jadiel Carlos » Sex Jan 19, 2018 02:35
- 0 Respostas
- 4185 Exibições
- Última mensagem por Jadiel Carlos

Sex Jan 19, 2018 02:35
Números Complexos
-
- Série geométrica
por lucasguilherme2 » Seg Ago 13, 2012 23:05
- 2 Respostas
- 1705 Exibições
- Última mensagem por lucasguilherme2

Ter Ago 14, 2012 00:30
Sequências
-
- Problema (Série Geométrica) - qual a resolução?
por MikeBlogger » Seg Nov 17, 2014 19:46
- 0 Respostas
- 2804 Exibições
- Última mensagem por MikeBlogger

Seg Nov 17, 2014 19:46
Progressões
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 3693 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 15 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
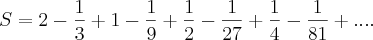

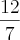

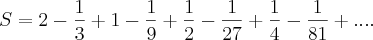

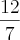

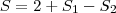
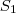 e
e 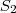 valem
valem
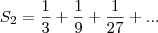
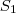 e
e 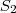 formam uma PG infinita, temos que
formam uma PG infinita, temos que
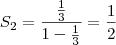
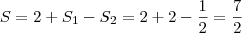
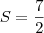

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)