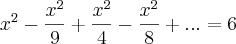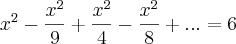por jose henrique » Sáb Out 09, 2010 18:03
por jose henrique » Sáb Out 09, 2010 18:03
os valores de x de modo que
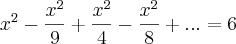
mas eu não consegui achar q, pois se pegarmos a2/a1= 1/9 se pegarmos a4/a3 = 1/2.
e para resolver está questão eu teria que achar o valor de q. o que faço?
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Elcioschin » Sáb Out 09, 2010 20:24
por Elcioschin » Sáb Out 09, 2010 20:24
Isto NÃO é uma PG. É uma série diferente.
Poderia até ser a soma de duas ou mais PGs. Para descobrir seria necessário conhecer pelo menos mais dois termos.
O enunciado é somente isto mesmo?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por jose henrique » Sáb Out 09, 2010 20:40
por jose henrique » Sáb Out 09, 2010 20:40
seria sim
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por DanielRJ » Sáb Out 09, 2010 21:23
por DanielRJ » Sáb Out 09, 2010 21:23
jose henrique escreveu:seria sim
acho que erram ai no lugar do 9 seria o 2
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Dom Out 10, 2010 13:19
por Elcioschin » Dom Out 10, 2010 13:19
Acho que o Daniel acertou na mosca:
x² - x²/2 + x²/4 - x²/8 = 6
x²*(1 - 1/2 + 1/4 - 1/8 + .....) = 6
Agora temos uma PG decrescente infinita de razão r = - 1/2 ----> S = a1/[1 - q] ----> S = 1/[1 - (-1/2)] ----> S = 1/(3/2) ----> S = 2/3
x²*(2/3) = 6 ----> x² = 3*6/2 ----> x² = 9 ----> x = +3 ou x = -3
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por jose henrique » Qui Out 28, 2010 22:47
por jose henrique » Qui Out 28, 2010 22:47
obrigado!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O limite da soma de um pg
por jose henrique » Sáb Out 09, 2010 17:45
- 6 Respostas
- 3068 Exibições
- Última mensagem por MarceloFantini

Sáb Out 09, 2010 21:29
Progressões
-
- Limite: Da soma
por Victor Gabriel » Sex Mai 10, 2013 11:49
- 0 Respostas
- 721 Exibições
- Última mensagem por Victor Gabriel

Sex Mai 10, 2013 11:49
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] soma de cubos
por beel » Dom Set 18, 2011 16:49
- 4 Respostas
- 2208 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:09
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] DÚVIDA - soma de quadrados
por beel » Dom Set 18, 2011 17:40
- 3 Respostas
- 1881 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2101 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.