Olá Joana. Pensemos primeiro no seguinte, estamos sempre somando 1 + 1 + 2 + 2 + 3 + 3 + ... ; ou seja estamos somando 2(1 + 2 + 3 + 4 + ... ). Sendo assim, é interessante procurarmos uma soma de números naturais que nos aproxime mais de 99. Sabemos que essa soma é dada por:

Lembrando que estamos somando dobrado, temos:
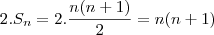
Após poucas tentativas, chegamos a n como sendo no máximo 9 (para n maior que 9, note que teremos 110 bandeiras, o que ultrapassaria o limite de 99). Esclarecendo um pouco mais, queremos descobrir quantas bandeiras foram postas, após a última soma "pareada" (que no caso é 9 vermelhas mais 9 azuis). Continuando:
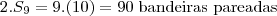
Obviamente, se seguirmos a sequência, deveremos somar mais 10 vermelhas, 10 azuis, etc. Como só temos 99, as últimas a serem somadas foram 9 vermelhas. Finalizando, vemos que o total de bandeiras azuis é metade das 90 bandeiras pareadas, ou seja, é de 45 (alternativa d).



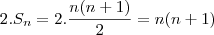
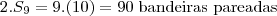

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.