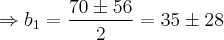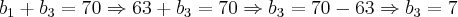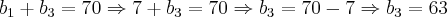Dados:
![\left({b}_{1}, \,\, {b}_{2}, \,\, {b}_{3} \right) \,\,\,\, PG \,\,\,\, [1] \left({b}_{1}, \,\, {b}_{2}, \,\, {b}_{3} \right) \,\,\,\, PG \,\,\,\, [1]](/latexrender/pictures/1fcdbb196e880aa9d63a2ae017f6df9b.png)
![\left({b}_{1} + 25, \,\, {b}_{2} + 27, \,\, {b}_{3} + 1 \right) \,\,\,\, PA \,\,\,\, [2] \left({b}_{1} + 25, \,\, {b}_{2} + 27, \,\, {b}_{3} + 1 \right) \,\,\,\, PA \,\,\,\, [2]](/latexrender/pictures/f9defcb4f26130a0a1c11675dd8b7d21.png)
![{b}_{1} + {b}_{2} + {b}_{3} = 91 \,\,\,\, [3] {b}_{1} + {b}_{2} + {b}_{3} = 91 \,\,\,\, [3]](/latexrender/pictures/61144fef1f07a82b58e81789934ee2f7.png)
q > 1
A razão da PG em [1] será:
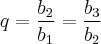
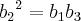
![{b}_{3} = \frac{{{b}_{2}}^{2}}{{b}_{1}} \,\,\,\,\, [4] {b}_{3} = \frac{{{b}_{2}}^{2}}{{b}_{1}} \,\,\,\,\, [4]](/latexrender/pictures/d03ead2799e60df1d7e00ff02faa74cc.png)
A razão na PA em [2] será:
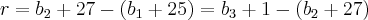
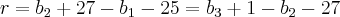


![2{b}_{2} - {b}_{1} - {b}_{3} = - 28 \,\,\,\, [5] 2{b}_{2} - {b}_{1} - {b}_{3} = - 28 \,\,\,\, [5]](/latexrender/pictures/5b29d71174754d0603dd7afbcfd4aabd.png)
Usando [3] em [5], observamos que:
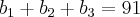
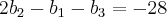
eles formam um sistema de equações e que, se somarmos ambas as equações, poderemos encontrar um dos valores. Somemos então as duas equações:
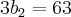
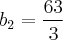
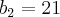
Agora, vamos substituir este valor em [3], [4] e [5]:
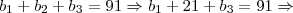
![\Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [6] \Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [6]](/latexrender/pictures/2cfd4d27e9afb1b0c15560145aa87e3f.png)
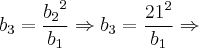
![\Rightarrow {b}_{3} = \frac{441}{{b}_{1}} \,\,\,\,\, [7] \Rightarrow {b}_{3} = \frac{441}{{b}_{1}} \,\,\,\,\, [7]](/latexrender/pictures/983daba84ffab533c733b991cb5bf6c1.png)
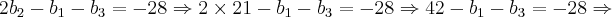
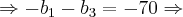
![\Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [8] \Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [8]](/latexrender/pictures/fc58cee74ad88215163861218859ada8.png)
Usando [7] em [6] ou [8], teremos:


Desta última equação (quadrática) obtemos:
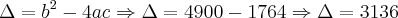
![\sqrt[]{\Delta} = 56 \sqrt[]{\Delta} = 56](/latexrender/pictures/b469ff0548c698035565b63efb85560d.png)
![{b}_{1} = \frac{-b \pm \sqrt[]{\Delta}}{2a} \Rightarrow {b}_{1} = \frac{-b \pm \sqrt[]{\Delta}}{2a} \Rightarrow](/latexrender/pictures/bdae0101167dbdb89c6fe5e9801e2088.png)
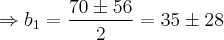

Com estes dois resultados, vamos agora obter através de [6] ou [8] o valor do terceiro termo da PA e da PG:
Usando 63 para o primeiro termo:
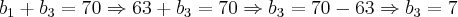
Usando 7 para o primeiro termo:
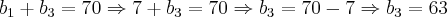
Agora, ficamos com estas duas possibilidades para a PG e a PA:
RESPOSTA 1:
PG - (63, 21, 7) => Razão: 1/3
PA - (63 + 25, 21 + 27, 7 + 1) = (88, 48, 8) => razão = -40
e
RESPOSTA 2:
PG - (7, 21, 63) => Razão: 3
PA - (7 + 25, 21 + 27, 63 + 1) = (32, 48, 64) => razão = 16
No enunciado, foi dado que a razão (q) deve ser maior que 1 (q > 1). Portanto, a única resposta possível para esta questão deverá ser a RESPOSTA 2, ou seja, o primeiro termo vale 7.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



![\left({b}_{1}, \,\, {b}_{2}, \,\, {b}_{3} \right) \,\,\,\, PG \,\,\,\, [1] \left({b}_{1}, \,\, {b}_{2}, \,\, {b}_{3} \right) \,\,\,\, PG \,\,\,\, [1]](/latexrender/pictures/1fcdbb196e880aa9d63a2ae017f6df9b.png)
![\left({b}_{1} + 25, \,\, {b}_{2} + 27, \,\, {b}_{3} + 1 \right) \,\,\,\, PA \,\,\,\, [2] \left({b}_{1} + 25, \,\, {b}_{2} + 27, \,\, {b}_{3} + 1 \right) \,\,\,\, PA \,\,\,\, [2]](/latexrender/pictures/f9defcb4f26130a0a1c11675dd8b7d21.png)
![{b}_{1} + {b}_{2} + {b}_{3} = 91 \,\,\,\, [3] {b}_{1} + {b}_{2} + {b}_{3} = 91 \,\,\,\, [3]](/latexrender/pictures/61144fef1f07a82b58e81789934ee2f7.png)
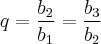
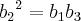
![{b}_{3} = \frac{{{b}_{2}}^{2}}{{b}_{1}} \,\,\,\,\, [4] {b}_{3} = \frac{{{b}_{2}}^{2}}{{b}_{1}} \,\,\,\,\, [4]](/latexrender/pictures/d03ead2799e60df1d7e00ff02faa74cc.png)
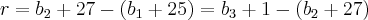
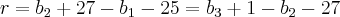


![2{b}_{2} - {b}_{1} - {b}_{3} = - 28 \,\,\,\, [5] 2{b}_{2} - {b}_{1} - {b}_{3} = - 28 \,\,\,\, [5]](/latexrender/pictures/5b29d71174754d0603dd7afbcfd4aabd.png)
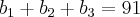
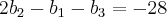
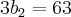
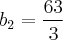
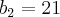
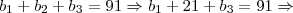
![\Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [6] \Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [6]](/latexrender/pictures/2cfd4d27e9afb1b0c15560145aa87e3f.png)
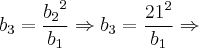
![\Rightarrow {b}_{3} = \frac{441}{{b}_{1}} \,\,\,\,\, [7] \Rightarrow {b}_{3} = \frac{441}{{b}_{1}} \,\,\,\,\, [7]](/latexrender/pictures/983daba84ffab533c733b991cb5bf6c1.png)
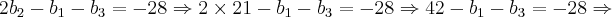
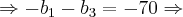
![\Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [8] \Rightarrow {b}_{1} + {b}_{3} = 70 \,\,\,\, [8]](/latexrender/pictures/fc58cee74ad88215163861218859ada8.png)


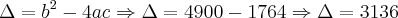
![\sqrt[]{\Delta} = 56 \sqrt[]{\Delta} = 56](/latexrender/pictures/b469ff0548c698035565b63efb85560d.png)
![{b}_{1} = \frac{-b \pm \sqrt[]{\Delta}}{2a} \Rightarrow {b}_{1} = \frac{-b \pm \sqrt[]{\Delta}}{2a} \Rightarrow](/latexrender/pictures/bdae0101167dbdb89c6fe5e9801e2088.png)