Zenildo,
Utilizar a fórmula da soma diretamente com base na sequência dada não funcionárá porque a sequência dada não é uma PG "pura", apesar de que, por coincidência, sua resposta seja a correta. Exemplo de uma PG:
(3, 6, 12, 24,...) onde 6/3 = 2, 12/6=2, 24/12 = 2, ou seja, a razão sempre e dois. O primeiro termos vale 3, o segundo seria 2 x 3 = 6, o terceiro termo 2 x 6 = 12 e assim por diante. Sempre estamos multiplicando por 2 neste caso e por isso é uma PG pura.
No caso da sequência que forneceu, ela ainda não é uma PG "pura" pois as razões se alteram de um termo para outro. No entanto, se separarmos alguns membros, formando conjuntos diferentes podemos dizer que ela é uma PG, mas do jeito que foi dada, ainda não é uma PG e por isso, as fórmulas para PG ainda não se aplicam.
Sendo sua sequêcia: (1,2,2,4,4,4,4, ..., 64,..., 64)
podemos formar outras sequências com alguns membros tais como:
(1, 2, 4, 8, 16, 32, 64) = 7 termos
(2, 4, 8, 16, 32, 64) = 6 termos
(4, 8, 16, 32, 64) = 5 termos
(4, 8, 16, 32, 64) = 5 termos
(8, 16, 32, 64) = 4 termos
(8, 16, 32, 64) = 4 termos
(8, 16, 32, 64) = 4 termos
(8, 16, 32, 64) = 4 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(16, 32, 64) = 3 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
(32, 64) = 2 termos
e por fim temos 64 aparecendo 32 vezes acima e portanto, ainda faltam aparecer mais 32 vezes para termos 64 sequencias com o 64 nele. Assim estão faltando 32 sequencias de (64)
Somando-se a quantidade termos de cada uma destas sequencias, teremos: 95 + os últimos 32 = 127 termos no total.
Vamos agora calcular de outra forma:
O número 1 aparece apenas uma vez.
O número 2 aparece 2 vezes
O número 4 aparece 4 vezes
O número 8 aparece 8 vezes
e assim por diante até
O número 64 aparece 64 vezes.
Logo se formarmos uma nova sequencia, teremos: (1, 2, 4, 8, 16, 32, 64) que é uma PG de razão 2
O número de termos dessa PG é 7. Cada termo desta nova PG representa a quantidade de termos na PG original. Assim, bastará que somemos tudo ou, que utilizemos a fórmula da Soma da PG nesta nova PG para termos o total de termos da PG original, ou seja:
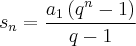
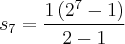
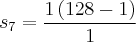
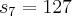
Portanto, o total de termos da sequencia original é 127. Como calculamos manualmente na primeira parte.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali


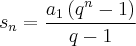
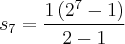
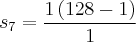
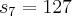

 .
.
 :
: