Olá
kotta.
É importante comentar as tentativas, mesmo que não tenham sido produtivas.
Resolvi o exercício no papel, mas antes de postar aqui, seguem algumas dicas:
1) Como a razão da P.G. é dada, você já pode escrever os 3 termos desta P.G. em função de

, ou seja:
P.G.
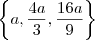
2) Analogamente, faça o mesmo para a P.A:
P.A.
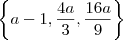
3) Agora, para resolver, note o seguinte:
Na P.G., a razão é um valor constante, sendo o
quociente entre um termo e seu antecessor.
Já na P.A., a razão também é constante, sendo a
diferença entre um termo e seu antecessor.
Então, aplique este conceito de razão de P.A. à nossa P.A. acima, igualando a diferença do segundo termo pelo primeiro, com a diferença do terceiro pelo segundo termo.
Fazendo assim, nesta igualdade, você terá uma equação do primeiro grau, com uma única variável que é exatamente o primeiro termo

, e você poderá encontrá-lo.
Conseqüentemente, poderá substituí-lo para encontrar

e

que estão em função de

.
Você deve encontrar estes valores:

,
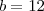
e
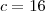
.
Nota: para conferir, teste os valores e verá que satisfazem as progressões citadas.




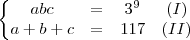
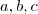 estão em progressão geométrica, com razão
estão em progressão geométrica, com razão  :
: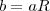
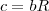
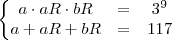

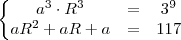

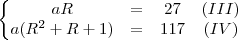
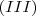 :
:
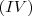 :
: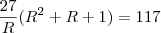
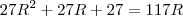
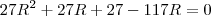
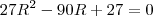
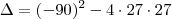
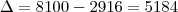
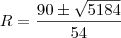
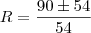
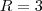 ou
ou 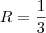

 :
:

 . Além disso, a-1, b, c, nessa ordem, estão em progressão aritmética a, b, c.
. Além disso, a-1, b, c, nessa ordem, estão em progressão aritmética a, b, c.![R=\frac{b}{a}= \frac{b}{c}
[tex]\frac{4}{3}=\frac{a*r}{a} R=\frac{b}{a}= \frac{b}{c}
[tex]\frac{4}{3}=\frac{a*r}{a}](/latexrender/pictures/46f0030565ca4ad8f0eb4ac038380eed.png)
 , ou seja:
, ou seja: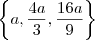
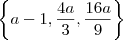
 e
e  que estão em função de
que estão em função de  ,
, 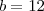 e
e 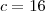 .
.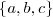 (com razão
(com razão  )
)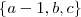 (a razão ainda não sabemos)
(a razão ainda não sabemos)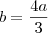
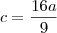
 a razão da P.A., então:
a razão da P.A., então: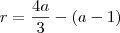
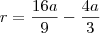
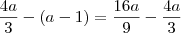

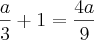
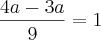
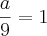


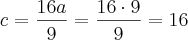
 .
. .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.