-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478291 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532955 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496452 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 709032 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2127252 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Jhenrique » Sáb Dez 22, 2012 16:56
por Jhenrique » Sáb Dez 22, 2012 16:56
Saudações caros!
Depois de descobrir que poderia relacionar PA e PG com funções polinomais e exponenciais, respectivamente, achei mais proveitoso trabalhar com tais funções a aquelas fórmulas e equações de progressões que, para mim, são abomináveis! Pretendo, então, fazer algumas demonstrações...
Em primeiro lugar, é necessário saber que uma PA de 1ª ordem se corresponde com a função afim: "y=ax+b", a de 2ª ordem com a função quadrática: "y=ax²+bx+c" e assim sucessivamente... Ademais, sabemos que essas funções são relacionadas através do cálculo diferencial e integral. Derivando uma função quadrática obtem-se uma função linear... se essas funções representam progressões então podemos facilmente saltar entre as ordens das mesmas!
Jás as PG de 1ª, 2ª e 3ª ordem... se correspondem respectivamente com as seguintes funções:
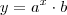
;
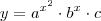
;
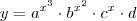
. Descobre-se a tx de variações dessas funções através da derivada geométrica:
![f^*(x)=\sqrt[dx]{dy} f^*(x)=\sqrt[dx]{dy}](/latexrender/pictures/cf5394db08e05adad1730623d0b141dd.png)
.
OK! ... Mas o que o cálculo tem a ver com progressões? Tudo! Em progressões, fala-se muito em diferença e em razão entre termos consecutivos, isto é a derivada da função (progressão) avaliada na média (em x) entre os termos escolhidos. Vejam os exemplos abaixos:
Bem, eu considero isso extramamente relevante, muito embora nunca vi nem ouvi essa explicação.
E o segundo ponto que tenho a dizer é que eu determinei uma fórmula que calcula o somatório entre termos consecutivos duma função polinomial e o produtório entre termos consecutivos duma função exponencial.
Dada uma função do tipo
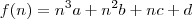
, a soma dos termos consecutivos é feita da seguinta maneira:
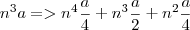
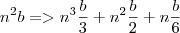
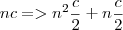
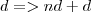
Mas como a função é
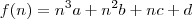
, então implica que o somatório dos termos consecutivos é:
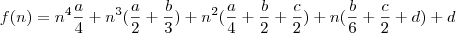
E para a função do tipo
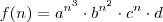
, o produtório entre os termos consecutivos é feito da seguinda maneira:
![a^{n^3}=>\sqrt[4]{a}^{n^4}\cdot\sqrt[2]{a}^{n^3}\cdot\sqrt[4]{a}^{n^2} a^{n^3}=>\sqrt[4]{a}^{n^4}\cdot\sqrt[2]{a}^{n^3}\cdot\sqrt[4]{a}^{n^2}](/latexrender/pictures/ce313bb767354176731abb61d500dbf3.png)
![b^{n^2}=>\sqrt[3]{b}^{n^3}\cdot\sqrt[2]{b}^{n^2}\cdot\sqrt[6]{b}^n b^{n^2}=>\sqrt[3]{b}^{n^3}\cdot\sqrt[2]{b}^{n^2}\cdot\sqrt[6]{b}^n](/latexrender/pictures/a7ed637bdee3e96deb47cc2bd4c2a913.png)
![c^n=>\sqrt[2]{c}^{n^2}\cdot\sqrt[2]{c}^n c^n=>\sqrt[2]{c}^{n^2}\cdot\sqrt[2]{c}^n](/latexrender/pictures/2d3ab81af46c7b5ae4bf8d556a116d52.png)
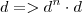
Mas como a função é
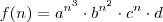
, então implica que o produtório dos termos consecutivos é totalmente análogo ao método do polinômio.
Fonte: Eu.
O que acham?
Até mais,
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Seg Dez 24, 2012 17:49
por Russman » Seg Dez 24, 2012 17:49
A relação de subtração dos termos consecutivos da função de 2° Grau de uma variável discreta é perfeitamente provável.
Seja

uma variável discreta e
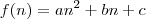
uma função desta variável.
O que você está fazendo é subtrair
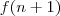
de
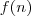
, isto é, você está calculando a diferença de termos consecutivos e afirma que
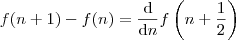
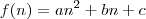
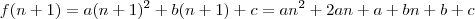
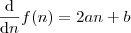
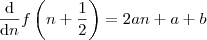
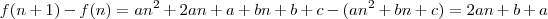
Como

, então podemos afirmar que existe a identidade dada por
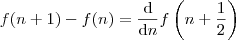
,
se
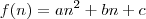
.
Tente provar o mesmo pra função exponencial...mas lembre-se que
http://www.wolframalpha.com/input/?i=%2 ... %5En%29%29pois a sua derivada exponencial está errada.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Qua Dez 26, 2012 17:37
por Jhenrique » Qua Dez 26, 2012 17:37
Fico contente por vc ter levado em consideração as minhas fórmulas e ter comprovado elas!
Mas a minha ideia quando elaborei esse esquema é para justamente fugir desta sua linha raciocínio, pois eu a acho pouco intuitiva. Não é que eu realmente não a acho intuitiva, é que da forma como eu demonstrei, penso que a ideia fica mais explícita e simples!
E as fórmulas para calcular os termos consecutivos, uma mão na roda, não é mesmo? Pois com a fórmula de Gaus só é possível cálcular a soma dos termos duma função linear cuja tx de variação é de 1 para 1, ao passo que com as minhas vc pode calcular a soma dos termos duma função afim, quadrática e cúbica!
Quanto a derivada, ela não está errada, veja isto:
http://en.wikipedia.org/wiki/Multiplicative_calculusLegal né?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Jhenrique » Seg Dez 31, 2012 23:11
por Jhenrique » Seg Dez 31, 2012 23:11
Russman, essa afirmação que eu fiz e que vc comprovou também é válida para as funções de grandezas x e y sendo inversamente proporcionais?
Eu estive tentando descobrir uma fórmula que me indicasse o somatório dos termos consecutivos da função (sequência)
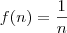
e comecei a ter sérias dificuldades. Então comecei a averiguar o problema e notei através do Geogebra que "a diferença entre termos consecutivos duma função é igual a sua derivada avaliada na média (em x) destes termos" não parece ser verdadeira para as funções de grandezas inversas, por exemplo:
Notou os valores destacados em azul no gráfico e na tabela? Observou como eles não coincidem? Eu fiz os cálculos pela M.A., pela M.G. dá uma aproximaçãozinha um pouco melhor, mas ainda assim não é exato.
Essa incoerência talvez seja a explicação do porque eu não consigo expressar o somatório dos termos da função f(n)=1/n como uma outra função.
Aguardo ansiosamente por mais comentários!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Que método usar para resolver esse problema?
por souzalucasr » Seg Mai 07, 2012 12:43
- 1 Respostas
- 1388 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 18:17
Cálculo: Limites, Derivadas e Integrais
-
- método de contagem
por sinuca147 » Seg Mai 25, 2009 09:10
- 2 Respostas
- 17601 Exibições
- Última mensagem por sinuca147

Seg Mai 25, 2009 23:35
Conjuntos
-
- Metodo de Gauss
por Jaison Werner » Seg Jan 10, 2011 19:11
- 3 Respostas
- 2569 Exibições
- Última mensagem por Renato_RJ

Ter Jan 18, 2011 23:42
Cálculo: Limites, Derivadas e Integrais
-
- Metodo de Jacobi
por Jaison Werner » Seg Jan 10, 2011 19:14
- 1 Respostas
- 1161 Exibições
- Última mensagem por Elcioschin

Ter Jan 11, 2011 22:18
Cálculo: Limites, Derivadas e Integrais
-
- Método da substituição
 por leticiapires52 » Ter Out 06, 2015 18:04
por leticiapires52 » Ter Out 06, 2015 18:04
- 2 Respostas
- 2664 Exibições
- Última mensagem por leticiapires52

Ter Out 06, 2015 20:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
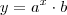 ;
; 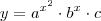 ;
; 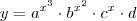 . Descobre-se a tx de variações dessas funções através da derivada geométrica:
. Descobre-se a tx de variações dessas funções através da derivada geométrica: ![f^*(x)=\sqrt[dx]{dy} f^*(x)=\sqrt[dx]{dy}](/latexrender/pictures/cf5394db08e05adad1730623d0b141dd.png) .
.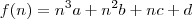 , a soma dos termos consecutivos é feita da seguinta maneira:
, a soma dos termos consecutivos é feita da seguinta maneira: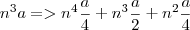
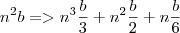
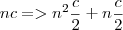
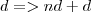
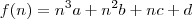 , então implica que o somatório dos termos consecutivos é:
, então implica que o somatório dos termos consecutivos é: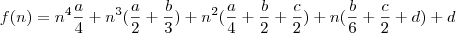
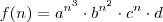 , o produtório entre os termos consecutivos é feito da seguinda maneira:
, o produtório entre os termos consecutivos é feito da seguinda maneira:![a^{n^3}=>\sqrt[4]{a}^{n^4}\cdot\sqrt[2]{a}^{n^3}\cdot\sqrt[4]{a}^{n^2} a^{n^3}=>\sqrt[4]{a}^{n^4}\cdot\sqrt[2]{a}^{n^3}\cdot\sqrt[4]{a}^{n^2}](/latexrender/pictures/ce313bb767354176731abb61d500dbf3.png)
![b^{n^2}=>\sqrt[3]{b}^{n^3}\cdot\sqrt[2]{b}^{n^2}\cdot\sqrt[6]{b}^n b^{n^2}=>\sqrt[3]{b}^{n^3}\cdot\sqrt[2]{b}^{n^2}\cdot\sqrt[6]{b}^n](/latexrender/pictures/a7ed637bdee3e96deb47cc2bd4c2a913.png)
![c^n=>\sqrt[2]{c}^{n^2}\cdot\sqrt[2]{c}^n c^n=>\sqrt[2]{c}^{n^2}\cdot\sqrt[2]{c}^n](/latexrender/pictures/2d3ab81af46c7b5ae4bf8d556a116d52.png)
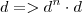
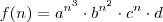 , então implica que o produtório dos termos consecutivos é totalmente análogo ao método do polinômio.
, então implica que o produtório dos termos consecutivos é totalmente análogo ao método do polinômio.

 uma variável discreta e
uma variável discreta e 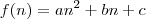 uma função desta variável.
uma função desta variável.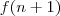 de
de 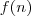 , isto é, você está calculando a diferença de termos consecutivos e afirma que
, isto é, você está calculando a diferença de termos consecutivos e afirma que 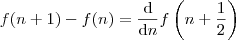
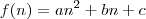
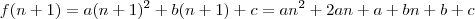
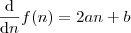
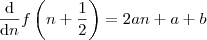
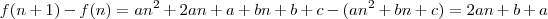
 , então podemos afirmar que existe a identidade dada por
, então podemos afirmar que existe a identidade dada por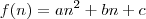 .
.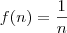 e comecei a ter sérias dificuldades. Então comecei a averiguar o problema e notei através do Geogebra que "a diferença entre termos consecutivos duma função é igual a sua derivada avaliada na média (em x) destes termos" não parece ser verdadeira para as funções de grandezas inversas, por exemplo:
e comecei a ter sérias dificuldades. Então comecei a averiguar o problema e notei através do Geogebra que "a diferença entre termos consecutivos duma função é igual a sua derivada avaliada na média (em x) destes termos" não parece ser verdadeira para as funções de grandezas inversas, por exemplo: } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: