 por e8group » Qui Nov 08, 2012 19:08
por e8group » Qui Nov 08, 2012 19:08
Alguém sabe onde encontro a demonstração abaixo , não quero apenas indução fraca ou forte . Quero desenvolver o lado esquerdo e chegar no lado direito da seguinte expressão .

.
Em seguida , vou deixar minha solução e gostaria de saber como vc's desenvolveriam .
Solução :

.
Mas ,

ou seja

.
Daí ,

.
Somando

em ambos lados da igualdade vamos obter que ,

e finalmente , multiplicando toda igualdade por
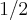
,

teremos que ,

.
Agora que cheguei no lado direito através do esquerdo , posso provar por indução que vale para n + 1 ou melhor ainda mostro que vale para n-1 e para n+1 .
OBS.: Alguém de vc's conhecem algum livro que posso deparar com exercícios como este acima e também sobre indução matemática .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qui Nov 08, 2012 19:17
por MarceloFantini » Qui Nov 08, 2012 19:17
Seja

. Somando ambas, temos

. Ao fazer isto efetuamos

somas, daí

e portanto

.
É a demonstração mais interessante que eu conheço. Nem tudo é possível desenvolver de um lado e chegar no outro.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Qui Nov 08, 2012 19:31
por e8group » Qui Nov 08, 2012 19:31
OK ! Na verdade esta eu fiz aqui também, realmente é muito boa , foi a primeira que fiz da mesma forma q vc . Mas ,como gostaria de fazer de uma outra forma que leve ao mesmo caminho optei por esta acima também . Na sua opinião , minha demostração também é aceita da mesma forma que a sua ?
Obrigado pela atenção .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Nov 08, 2012 20:32
por e8group » Qui Nov 08, 2012 20:32
Marcelo , esta demonstração abaixo é a outra que eu fiz também , como relatei antes . Note que é a mesma coisa que vc fez , só utilizei somatório por ser compacto .

Portanto ,

OBS.:

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma de termos
por apotema2010 » Sex Fev 26, 2010 17:22
- 5 Respostas
- 6313 Exibições
- Última mensagem por Cleyson007

Dom Fev 28, 2010 08:50
Progressões
-
- Soma dos termos de uma PA
por 404040 » Dom Out 17, 2010 21:39
- 2 Respostas
- 3475 Exibições
- Última mensagem por 404040

Seg Out 18, 2010 17:55
Progressões
-
- Soma de termos P.A
por lucas7 » Seg Jun 27, 2011 18:34
- 1 Respostas
- 1645 Exibições
- Última mensagem por Neperiano

Seg Jun 27, 2011 19:37
Progressões
-
- [P.A] DETERMINAR A SOMA ODS 60 PRIMEIROS TERMOS
por ramonalado » Ter Mar 12, 2013 23:35
- 3 Respostas
- 12904 Exibições
- Última mensagem por Russman

Qua Mar 13, 2013 22:46
Progressões
-
- [retas perpendiculares] soma dos termos independentes
por JKS » Qua Ago 01, 2012 13:36
- 2 Respostas
- 3115 Exibições
- Última mensagem por JKS

Qua Ago 08, 2012 15:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.  .
.  ou seja
ou seja  .
.  .
.  em ambos lados da igualdade vamos obter que ,
em ambos lados da igualdade vamos obter que , 
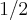 ,
, 
 .
. 

 . Somando ambas, temos
. Somando ambas, temos  . Ao fazer isto efetuamos
. Ao fazer isto efetuamos  somas, daí
somas, daí 
 .
.




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
