Olá, caro Guedes e amigos da matemática,
Para podermos responder a sua questão, temos que entender a pergunta: "... o número dessa colmeia se estabilizará em quantas abelhas?". O que se entende: em quanto a população de abelhas não variará? Isso quer dizer, a quantidade em que não haverá aumento ou diminuição no número total de abelhas, o que não quer dizer que não morram ou não nasçam abelhas, mas que a quantidade de nascimentos seja igual a quantidade mortes. Entendido isso, continuemos.
A sua questão, na verdade, envolve duas Progressõess Aritiméticas, e há de se considerar apenas uma no final. Vejamos.
1ª P.A.
A colmeia tem 8000 abelhas, logo

, destas a cada dia que passa morrem 200, logo r = -200.
Montando a equação do termo geral da P.A., temos:

,

Para sabermos o número de dias necessários para a extinção total, ou seja,

, dessa população de 8000 abelhas, isolamos o "n" da seguinte forma:
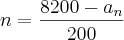
, logo,

,

. Isso quer dizer que no 41° dia, essa população chegará a zero.
2ª P.A.
À partir do 21° dia, nascem duas mil abelhas diariamente. Logo

(utilizamos 21 para facilitar os cálculos e a compreensão, mas não quer dizer que haja os termos de
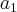
ao
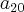
), e

.
Montando a equação do termo geral da P.A., temos:

,

,

.
Ora, se quarenta dias depois passam a morrer 2000 abelhas cada dia, do total de abelhas teremos que subtrair 2000 diáriamente. Considerando que isso irá ocorrer a partir do 60° dia (iniciando a contagem com o 21° dia, quarenta dias de vida se concluirá no 60° dia), obteremos uma população constante de abelhas, conforme compreensão apresentada no início, teremos então o seguinte cálculo:

, logo:
 Obs.: Verifique que a establização da população ocorre no 60° dia, ou seja, 19 dias após a extinção das 8000 abelhas iniciais, o que significa que elas não interferem na solução da questão, mas foi desenvolvida a sua P.A. a fim de sabermos o dia certo de sua extinção.
Obs.: Verifique que a establização da população ocorre no 60° dia, ou seja, 19 dias após a extinção das 8000 abelhas iniciais, o que significa que elas não interferem na solução da questão, mas foi desenvolvida a sua P.A. a fim de sabermos o dia certo de sua extinção.Caso ainda haja alguma dúvida, pode perguntar.


 , destas a cada dia que passa morrem 200, logo r = -200.
, destas a cada dia que passa morrem 200, logo r = -200. ,
, 
 , dessa população de 8000 abelhas, isolamos o "n" da seguinte forma:
, dessa população de 8000 abelhas, isolamos o "n" da seguinte forma: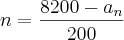 , logo,
, logo,  ,
,  . Isso quer dizer que no 41° dia, essa população chegará a zero.
. Isso quer dizer que no 41° dia, essa população chegará a zero. (utilizamos 21 para facilitar os cálculos e a compreensão, mas não quer dizer que haja os termos de
(utilizamos 21 para facilitar os cálculos e a compreensão, mas não quer dizer que haja os termos de 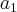 ao
ao 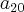 ), e
), e  .
. ,
,  ,
,  .
. , logo:
, logo:


 .
.



