 por Douglasm » Sex Out 01, 2010 16:20
por Douglasm » Sex Out 01, 2010 16:20
Só continue, divida 4088 por 8 e encontrará n = 9.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Sex Out 01, 2010 16:44
por DanielRJ » Sex Out 01, 2010 16:44
Douglasm escreveu:Só continue, divida 4088 por 8 e encontrará n = 9.
é mesmo esqueci de desenvolvero 2^3 vlw
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4260 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4730 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25582 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4244 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2899 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
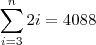
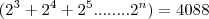
![Sn=\frac{a_1[q^n-1]}{q-1} Sn=\frac{a_1[q^n-1]}{q-1}](/latexrender/pictures/3f353d20dae73fa7a0dc9cb1cc826fbb.png)
![\frac{2^3[2^n-1]}{2-1}=4088 \frac{2^3[2^n-1]}{2-1}=4088](/latexrender/pictures/db51fbb9c2f037df955b2f675a149f86.png)
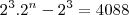 Cheguei nesta parte e não sei o que fazer.. alguem me ajude ai.
Cheguei nesta parte e não sei o que fazer.. alguem me ajude ai.
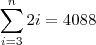
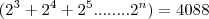
![Sn=\frac{a_1[q^n-1]}{q-1} Sn=\frac{a_1[q^n-1]}{q-1}](/latexrender/pictures/3f353d20dae73fa7a0dc9cb1cc826fbb.png)
![\frac{2^3[2^n-1]}{2-1}=4088 \frac{2^3[2^n-1]}{2-1}=4088](/latexrender/pictures/db51fbb9c2f037df955b2f675a149f86.png)
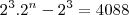 Cheguei nesta parte e não sei o que fazer.. alguem me ajude ai.
Cheguei nesta parte e não sei o que fazer.. alguem me ajude ai.


