 por jolie » Qui Out 29, 2009 10:31
por jolie » Qui Out 29, 2009 10:31
Não estou enviando tentativas pois não tenho a minima idéia de como resolver.
As raízes da equação x³+9kx²+nx+m=0 formam uma P.A. de razão 3. qual é o valor de m e n?
-
jolie
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Out 29, 2009 10:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Elcioschin » Sáb Out 31, 2009 10:11
por Elcioschin » Sáb Out 31, 2009 10:11
Raízes ---> a, a + 3, a + 6
Pelas Relações de Girard:
a + (a + 3) + (a + 6) = - 9k/1 -----> 3a + 9 = - 9k ----> a + 3 = - 3k ----> a = - 3(k + 1) -----> Equação I
a*(a + 3) + a*(a + 6) + (a + 3)*(a + 6) = n/1 ----->n = 3a² + 18a + 18 -----> Equação II
a*(a + 3)*(a + 6) = - m/1 -----> a³ + 9a² + 18a = - m ----> m = a³ + 9a² + 18a ----> Equação III
Basta agora subsituir a da equação I nas equações II e III e se obtém m, n em função de k
Editado pela última vez por
Elcioschin em Sáb Out 31, 2009 12:54, em um total de 1 vez.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Cleyson007 » Sáb Out 31, 2009 12:00
por Cleyson007 » Sáb Out 31, 2009 12:00
Bom dia Jolie e Elcioschin!
A dica do Elcio foi ótima.. pelas Relações de Girard, os valores de m e n podem ser encontrados.
Não sei se você conhece as
Relações de Girard (basta trabalhar com as raízes da equação), veja só:
Lembrando que as raízes da equação são: (a; a+3; a+6) --> O enunciado diz que elas formam um P.A. de razão 3.
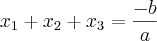
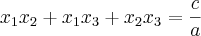
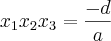
Substituindo
a na 1ª equação, encontra-se:
Para n -->
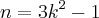
Quanto ao valor de m -->
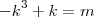
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




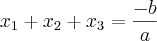
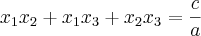
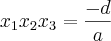
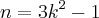
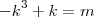




 , avisa que eu resolvo.
, avisa que eu resolvo.

