 por JKS » Qui Abr 11, 2013 01:11
por JKS » Qui Abr 11, 2013 01:11
preciso de ajuda,desde já agradeço!
Consideremos a PA (a1,a2,...,a5) e a PG (b1,b2,...,b5), ambas formadas por números inteiros , de mesma razão (r=q), sendo a1=b1. Se a5 = 11 e b2-a2=1, calcule b5.
GABARITO : 48
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Qui Abr 11, 2013 18:44
por young_jedi » Qui Abr 11, 2013 18:44
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por JKS » Dom Abr 21, 2013 18:07
por JKS » Dom Abr 21, 2013 18:07
Obrigada mesmo !!

me ajudou muito ..
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relação entre cordas entre dois pontos de retas.
por janderson77 » Seg Dez 02, 2013 12:00
- 0 Respostas
- 2063 Exibições
- Última mensagem por janderson77

Seg Dez 02, 2013 12:00
Trigonometria
-
- relação entre x e y
por Apotema » Qua Nov 18, 2009 19:57
- 4 Respostas
- 5878 Exibições
- Última mensagem por Apotema

Seg Nov 23, 2009 08:12
Trigonometria
-
- relação entre a e b
por jose henrique » Seg Set 13, 2010 09:31
- 3 Respostas
- 4724 Exibições
- Última mensagem por Elcioschin

Ter Set 14, 2010 10:45
Álgebra Elementar
-
- relação entre conjuntos
por Julivanny » Sex Set 12, 2008 12:46
- 1 Respostas
- 3450 Exibições
- Última mensagem por admin

Ter Set 16, 2008 17:44
Conjuntos
-
- Relação entre pi e radiano
por studieren » Sex Jan 01, 2010 23:03
- 1 Respostas
- 5181 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 02, 2010 02:05
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




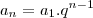
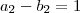 e r=q temos que
e r=q temos que
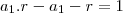
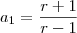
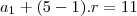
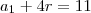
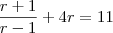
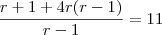
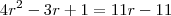
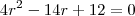
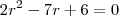

 me ajudou muito ..
me ajudou muito ..
