 por GABRIELFLA » Sáb Abr 20, 2013 23:09
por GABRIELFLA » Sáb Abr 20, 2013 23:09
Numa P.G, a diferença entre o 3° termo e o 1° termo é 99/40 , e a diferença entre o 4° eo 2° termo é 99/4.Qual é a razão dessa P.G? Determine a sequência.
-
GABRIELFLA
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 20, 2013 22:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por ant_dii » Sáb Abr 20, 2013 23:48
por ant_dii » Sáb Abr 20, 2013 23:48
Bom GABRIELFLA , é relativamente simples
basta lembrar que

Veja que você precisa de

Então, vamos lá. Devemos fazer

Veja que da expressão de baixo podemos fazer

Mas a expressão de dentro do parenteses é

De onde você conclui que

Logo,

.
Pronto, você já tem a razão, agora substitua em qualquer uma das expressões do sistema feito acima e você irá encontrar
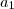
e, como consequência, poderá encontrar a sequência.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4260 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4729 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25579 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4244 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2897 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









 .
.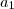 e, como consequência, poderá encontrar a sequência.
e, como consequência, poderá encontrar a sequência.
