As medidas dos lados de um retângulo e sua diagonal formam, nessa ordem, uma PA. Sabendo=se que o perímetro desse retângulo é igual a 14, determine a área desse retângulo.
Questão muito simples mas não sei fazer uma conta com os lados e diagonais formando uma PA. Me ajudem?





 e
e  os lados do retângulo e
os lados do retângulo e 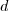 sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que
sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que  .
. ou
ou  .
. .
. e
e  segue que
segue que .
. .
.


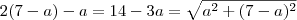 .
. , daí
, daí  e
e  .
.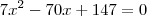 ?
?![\sqrt[]{{x}^{2}+{(7-x)}^{2}}=14-3x \sqrt[]{{x}^{2}+{(7-x)}^{2}}=14-3x](/latexrender/pictures/275e9d5d842fecef10f122d6c590af37.png)