 por Lucio » Ter Out 30, 2012 08:12
por Lucio » Ter Out 30, 2012 08:12
Olas colegas...
Se enumeram de 1 até n as páginas de um livro. Ao somar esses números, por engano, um deles é somado
duas vezes, obtendo-se o resultado incorreto: 1986. O valor de n e o número da página que foi
somado duas vezes são?
1º - Tentei por soma de PA, não consegui;
2º - Tentei pela fórmula =
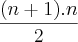
pois é um número triangular,
percebi que estava trabalhando com a soma de PA e não cheguei ao resultado.
Será que tem um outro caminho para a resolução?
Desde já agradeço a atenção de todos
Abraços
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por Cleyson007 » Ter Out 30, 2012 09:40
por Cleyson007 » Ter Out 30, 2012 09:40
A sequência das páginas do livro formam uma P.A de n termos e 1°termo igual a 1. Logo:
S = (n² + n)/2
Considerando que não houvesse a inclusão do número repetido, teríamos:
(n² + n)/2 = 1686
n² + n = 2 (1686) = 3372
n² + n - 3372 = 0
Por Bháskara, temos:
? = 1² - 4*(-3372) = 1 + 13488 = 13489
?? = ?13489 = ±116,14...
Pelo fato de ter tido acréscimo do número repetido, vemos que ?? deverá ser 116 ou 115. Logo:
n = (-1 + 116)/2 ou (-1 + 115)/2
Cujos resultados seriam
n = 115/2 ou 114/2.
Ora, o primeiro deles não serve, pois resultaria em um "n" fracionário; logo,
n = 114/2
n = 57
Quanto ao número da página que foi somado duas vezes:
S = (1 + 57)*57/2 = 58*57/2 = 58/2 * 57 = 29*57 = 1653
1686 - 1653 = 33
Solução:
n = 57
nº da página = 33
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por young_jedi » Ter Out 30, 2012 11:57
por young_jedi » Ter Out 30, 2012 11:57
eu encontrei como resposta n=62
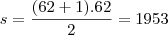
temos que
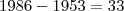
portanto o livro pode ter 62 paginas e ter somando por engano duas vezes a pagina 33
Na resposta do Cleyson ele utilizou 1686 mais o correto é 1986 mais o procedimento para se chegar na resposta é esse mesmo
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Lucio » Ter Out 30, 2012 13:13
por Lucio » Ter Out 30, 2012 13:13
Cleyson007 e Young_jedi.
Muito obrigado pelo apoio.
Abraços.
-
Lucio
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Dez 21, 2011 07:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6139 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4729 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5631 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4427 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8402 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
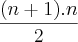 pois é um número triangular,
pois é um número triangular,



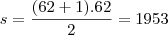
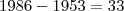
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
