 por Rafael16 » Qua Jul 18, 2012 19:48
por Rafael16 » Qua Jul 18, 2012 19:48
Olá pessoal,
não entendi como faz para calcular dízimas periódicas, por exemplo 0,3111...
sei como transformar em fração, que fica 28/90
Tentei resolver dessa forma:
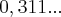

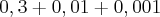
...

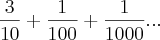
Calculei a razão que deu
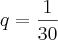
Depois coloquei na fórmula da soma infinita:
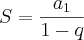

Resposta do livro:
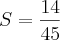
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Qua Jul 18, 2012 19:55
por Russman » Qua Jul 18, 2012 19:55
Você calculou a razão errado. Tente dividir o quarto termo pelo terceiro e verifique se dá os 3/10. Não dará.
O que você deve fazer é considerar a dízima como 0,3 + {PG}, pois inculindo o 0,3 na sequência esta não será uma P.G..
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Rafael16 » Qua Jul 18, 2012 20:04
por Rafael16 » Qua Jul 18, 2012 20:04
Russman escreveu:Você calculou a razão errado. Tente dividir o quarto termo pelo terceiro e verifique se dá os 3/10. Não dará.
O que você deve fazer é considerar a dízima como 0,3 + {PG}, pois inculindo o 0,3 na sequência esta não será uma P.G..
Ah sim, agora consegui, valeu Russman!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Russman » Qua Jul 18, 2012 21:20
por Russman » Qua Jul 18, 2012 21:20
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dizima periodica composta
por creberson » Sex Mai 24, 2019 11:03
- 1 Respostas
- 9637 Exibições
- Última mensagem por DanielFerreira

Qui Set 12, 2019 23:19
Conjuntos
-
- IME-96 Função periódica
por Balanar » Sáb Ago 07, 2010 17:58
- 4 Respostas
- 10894 Exibições
- Última mensagem por kamillanjb

Ter Mar 15, 2011 22:57
Desafios Difíceis
-
- Dízima
por Cristina Lins » Qui Abr 06, 2017 10:47
- 0 Respostas
- 7431 Exibições
- Última mensagem por Cristina Lins

Qui Abr 06, 2017 10:47
Álgebra Elementar
-
- [Sequência convergente e periódica ] Prove ...
por e8group » Seg Jan 20, 2014 23:45
- 0 Respostas
- 8451 Exibições
- Última mensagem por e8group

Seg Jan 20, 2014 23:45
Sequências
-
- Encontre a fração geratriz da dizima 1,777....
por andersontricordiano » Qua Abr 13, 2011 22:07
- 1 Respostas
- 9492 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:21
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
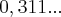

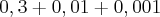 ...
...
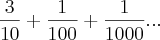
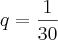
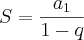

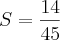




 .
.



