Dúvida em Exercício

[LuizCarlos]

Olá amigos, não estou conseguindo entender esse exercício!

3) Você já sabe que a fórmula da área de um triângulo em função da base e da altura relativa a essa base é A = .

a) Escreva uma fórmula para a área do triângulo ABC quando b = 13 cm.


A =

b) Escreva três pares ordenados (h, A), que sejam soluções da fórmula que você escreveu no item a.

, sendo A = 52 ; 40 ; 22












c) Escreva uma fórmula para a base b, quando a área do triângulo ABC .


Esse item c) não consegui entender.

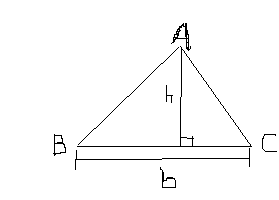
Triângulo03.png (3 KiB) Exibido 2583 vezes

[Lucio Carvalho]

Olá LuizCarlos,

Se A = 15 cm2, então:

15 = b.h/2 <-> 30 = b.h <-> b = 30/h

Portanto, sendo a área do triângulo constante, existe uma relação de proporcionalidade inversa entre a base e a altura.

Espero ter ajudado.

[LuizCarlos]

Olá LuizCarlos,

Se A = 15 cm2, então:

15 = b.h/2 <-> 30 = b.h <-> b = 30/h

Portanto, sendo a área do triângulo constante, existe uma relação de proporcionalidade inversa entre a base e a altura.

Espero ter ajudado.

Não entendi, mas obrigado por ter tentando ajudar!

[MarceloFantini]

Sua resposta do item (a) está correta, sua resolução do item (b) está incompleta. Você só fez a primeira parte do primeiro valor, que é encontrar o primeiro número do par ordenado. Como o exercício pediu, a resposta deve ser , onde e . Faça os outros da mesma forma.

Para o item (c), vamos começar igualando a expressão da área com o valor dado: . Agora, vamos multiplicar por 2 ambos lados: e chegamos em . Queremos uma expressão para a base , logo vamos isolá-lo: .