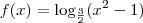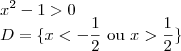-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 479789 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 537446 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501169 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 721376 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2154115 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Thassya » Sex Mai 29, 2009 11:26
por Thassya » Sex Mai 29, 2009 11:26
me ajudem a resolver essas duas questoes por favor:
1)Determine o domínio da funçao dada pela relaçao f(x)=log de (x ao quadrado - 1) na base 3/2.
2)Simplifique a expressão: (2 elevado a 8 - 2 elevado a 4 /2 elevado a 4 )elevado a -1 vezes 5
-
Thassya
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 21, 2009 23:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Cleyson007 » Sex Mai 29, 2009 12:00
por Cleyson007 » Sex Mai 29, 2009 12:00
Olá, bom dia!
Você tem o gabarito das questões?
Se tiver, coloque no fórum a fim de facilitar a vida de quem se dispõe a ajudá-la, ok?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Thassya » Sex Mai 29, 2009 18:04
por Thassya » Sex Mai 29, 2009 18:04
não tenho o gabarito não ...essas questões são um exercicio q vele ponto pra média da nota final...ajuda ai...
-
Thassya
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 21, 2009 23:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Cleyson007 » Dom Mai 31, 2009 17:13
por Cleyson007 » Dom Mai 31, 2009 17:13
Boa tarde Thassya!
Quanto a questão b, o que você quer calcular é:
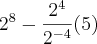
?
Se for isso, faça o seguinte:
Primeiramente,
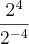
é o mesmo que
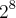
Agora, preciso que você confira o que está sendo multiplicado por 5 (é somente o termo que vem depois do sinal de - ou os dois termos)
Se for os dois termos, fica assim:
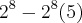
e o resultado será

.
Se for somente o termo que vem depois do sinal de -, fica assim:
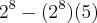
e o resultado será

Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Marcampucio » Dom Mai 31, 2009 18:58
por Marcampucio » Dom Mai 31, 2009 18:58
Determinar o domínio de
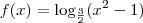
como condição de existência de um logarítimo
em qualquer base, o logaritimando deve ser maior que zero. Portanto
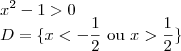
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [descobrir valor para domínio] Domínio da função
por Zebra-LNX » Sáb Jun 16, 2012 12:26
- 1 Respostas
- 2753 Exibições
- Última mensagem por MarceloFantini

Ter Jun 19, 2012 22:18
Funções
-
- [Domínio] Determinar domínio a partir da função
por +danile10 » Qui Fev 07, 2013 21:33
- 1 Respostas
- 2465 Exibições
- Última mensagem por e8group

Qui Fev 07, 2013 22:38
Funções
-
- [Domínio da Função] A função abaixo é definida f(x)=x²-3x
por Tiago Neto » Qui Mai 30, 2013 20:58
- 0 Respostas
- 1488 Exibições
- Última mensagem por Tiago Neto

Qui Mai 30, 2013 20:58
Funções
-
- Domínio de uma função
por Jonatan » Qui Jul 29, 2010 15:46
- 0 Respostas
- 1635 Exibições
- Última mensagem por Jonatan

Qui Jul 29, 2010 15:46
Funções
-
- domínio da função
por jose henrique » Ter Out 26, 2010 23:37
- 5 Respostas
- 2537 Exibições
- Última mensagem por jose henrique

Qui Out 28, 2010 22:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





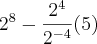 ?
?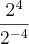 é o mesmo que
é o mesmo que 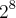
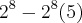 e o resultado será
e o resultado será  .
.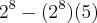 e o resultado será
e o resultado será