bom... decágono inscrito no circulo trigonométrico, tal que um vertice corresponde a pi/4
seguinte, voce pode determinar uma equação geral, é simples.
Imagine o decágono inscrito no circulo trigonométrico e o angulo focado em
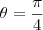
aonde se situa uma das arestras...
Voce concorda que se eu somar
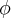
, para algum
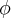
especifico, eu consigo chegar no proximo vértice?
ou seja, se
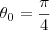
entao
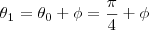
e obviamente
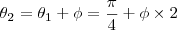
em fim...
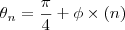
só nos resta saber quem é
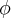
o que sabemos com toda certeza sobre o decágono?
sabemos que
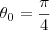
e que
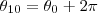
pela formula
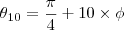
e ao mesmo tempo,
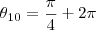
entende aonde quero chegar ?
com isso, conseguimos uma formula explícita para qualquer angulo relacionado a qualquer vetice no seu decágono...
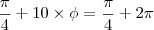
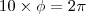
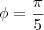
portanto a formula geral é:
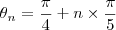
que vai corresponder a letra b) caso voce queira dizer com:
5pi + 4kpi/20
na verdade
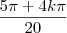


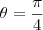 aonde se situa uma das arestras...
aonde se situa uma das arestras...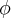 , para algum
, para algum 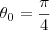
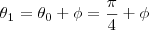
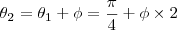
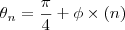
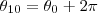
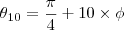
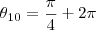
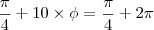
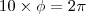
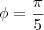
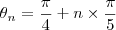
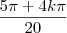


 .
.



