 por Andromeda » Seg Set 19, 2011 20:19
por Andromeda » Seg Set 19, 2011 20:19
FAAP
Resolver a equação tgx - 2senx = 0 para
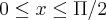
Eu comecei com:
tgx = 2senx (/senx)
1/cosx = 2
cos x = 1/2
Resposta: V{ Pi/3}
Mas o livro dá como resposta
V{0; Pi/3}
E agora? O que fiz de errado ou não visualizei?
-
Andromeda
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jul 27, 2011 13:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biomedicina
- Andamento: cursando
 por gvm » Seg Set 19, 2011 21:07
por gvm » Seg Set 19, 2011 21:07
Bom, não sei exatamente o que tem de errado na sua resolução. Mas nas equações trigonométricas em geral você tem que tomar muito cuidado quando for dividir, pois seno, cosseno e tangente podem ser iguais a zero aí dá problema no resultado. Deve ter dado algum problema na hora em que você dividiu tudo por sen x ali, é a única explicação que eu posso imaginar.
Eu resolvi da seguinte maneira e cheguei a uma resposta igual à do gabarito.
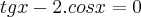
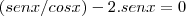
Colocando sen x em evidência:
![sen x [(1/cos x) - 2] = 0 sen x [(1/cos x) - 2] = 0](/latexrender/pictures/c51ffe705ba41712cb61f7c170a6ca64.png)
Para o resultado de uma multiplicação ser zero, um dos fatores obrigatoriamente é igual a 0, então:
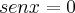

ou
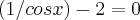

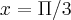
S = {0 ; pi/3}
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
 por Andromeda » Seg Set 19, 2011 21:13
por Andromeda » Seg Set 19, 2011 21:13
Putz! Tem razão...eu nem tinha me tocado de que senx, cosx e tgx pode dar zero...Acho que por isso estou errando uma 'porrada' de exercícios...Tenso viu?
Brigada, viu?
-
Andromeda
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jul 27, 2011 13:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biomedicina
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2548 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3391 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
-
- lim x^2.sin(x/1), x=0. Alguém pode me ajudar?
por Arthur_Bulcao » Seg Abr 09, 2012 18:05
- 2 Respostas
- 2012 Exibições
- Última mensagem por fraol

Seg Abr 09, 2012 19:24
Cálculo: Limites, Derivadas e Integrais
-
- Alguém pode me ajudar?
por Cleyson007 » Qui Out 11, 2012 09:18
- 2 Respostas
- 4060 Exibições
- Última mensagem por Cleyson007

Qui Out 11, 2012 11:38
Pedidos de Materiais
-
- Alguém pode me ajudar com ''Conjuntos''
por Alessander » Sáb Set 03, 2011 12:45
- 1 Respostas
- 2544 Exibições
- Última mensagem por Neperiano

Sáb Set 03, 2011 21:20
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
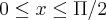

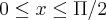

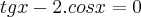
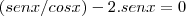
![sen x [(1/cos x) - 2] = 0 sen x [(1/cos x) - 2] = 0](/latexrender/pictures/c51ffe705ba41712cb61f7c170a6ca64.png)
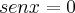

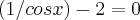

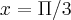


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.