 por Pre-Universitario » Qui Ago 11, 2011 17:31
por Pre-Universitario » Qui Ago 11, 2011 17:31
Um cowboy joga uma moeda para o alto. Quando a moeda atinge sua
altura maxima. ele da um tiro nela, com braço inclinado 60 graus em relaççao ao solo,
acertando-a. A moeda começa a cair em linha reta, perpendicularmente ao solo, e, com o braço
inclinado 45 graus em relação ao solo, o cowboy acerta mais um tiro nela. Sabendo que entre
um tiro e outro a moeda caiu 12 m, e que a altura do revolver em relação ao solo na hora dos dois disparos
era de 2 m, qual a altura maxima alcançada pela moeda?
Bom ! eu faço e refaço mas ñ chego nessa resposta
![20+6\sqrt[]{3} 20+6\sqrt[]{3}](/latexrender/pictures/d6ce4c5798c2c32cda0c573597155efc.png)
Gostaria que alguem resolvesse essa questão por favor
obrigado
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
 por LuizAquino » Qui Ago 11, 2011 20:33
por LuizAquino » Qui Ago 11, 2011 20:33
Primeiro comentário: do ponto de vista físico, essa questão está mal colocada.
Ignorando uma porção de leis da Física, esse exercício tenta descrever algo como ilustra a figura abaixo.
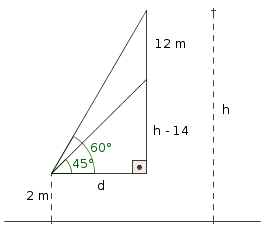
- altura_da_moeda.png (4.74 KiB) Exibido 3586 vezes
Podemos então escrever o sistema:
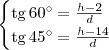
Isso é o mesmo que:
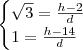
Da segunda equação, temos que
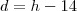
.
Podemos então reescrever a primeira equação como
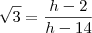
. Resolvendo essa equação, obtemos
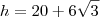
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Pre-Universitario » Sex Ago 12, 2011 17:22
por Pre-Universitario » Sex Ago 12, 2011 17:22
valeu por responder
estou respondendo algumas questões do livro
luiz roberto dante
livro:matematica "contexto e aplicações" primeiro Ano
lançado em 2006 se qizer da uma olhada no livro
é so ir há um bilbioteca blz
valeu
-
Pre-Universitario
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Sex Ago 05, 2011 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 3
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![20+6\sqrt[]{3} 20+6\sqrt[]{3}](/latexrender/pictures/d6ce4c5798c2c32cda0c573597155efc.png)


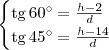
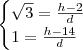
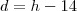 .
.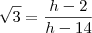 . Resolvendo essa equação, obtemos
. Resolvendo essa equação, obtemos 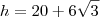 .
.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.