 por adauto martins » Sex Nov 15, 2019 11:01
por adauto martins » Sex Nov 15, 2019 11:01
(ITA-exame 1950)
resolver a equaçao
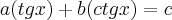
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
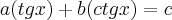

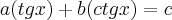

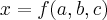
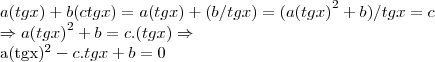
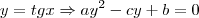
![{y}_{(1,2)}=(c/2a)(+,-)(\sqrt[]{\Delta})/2a)
{y}_{1}=(c/2a)+(\sqrt[]{\Delta}/2a)\Rightarrow
tgx=(c/2a)+(\sqrt[]{\Delta}/2a)
x=arctg((c/2a)+(\sqrt[]{\Delta}/2a)) {y}_{(1,2)}=(c/2a)(+,-)(\sqrt[]{\Delta})/2a)
{y}_{1}=(c/2a)+(\sqrt[]{\Delta}/2a)\Rightarrow
tgx=(c/2a)+(\sqrt[]{\Delta}/2a)
x=arctg((c/2a)+(\sqrt[]{\Delta}/2a))](/latexrender/pictures/e2f7aa3fff89c0445a40fc107d555379.png)
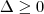
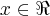
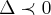
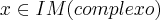
![x=arctg((c/2a)+(\sqrt[]{{c}^{2}-4ab}/2a)=arctg((c/2a)+\sqrt[]{({c}^{2}-4ab})/4{a}^{2}}) x=arctg((c/2a)+(\sqrt[]{{c}^{2}-4ab}/2a)=arctg((c/2a)+\sqrt[]{({c}^{2}-4ab})/4{a}^{2}})](/latexrender/pictures/972881aade1c2532ac89760f141aaa84.png)
![x=arctg((c/2a)+\sqrt[]{{(c/2a)}^{2}-(b/a)})=... x=arctg((c/2a)+\sqrt[]{{(c/2a)}^{2}-(b/a)})=...](/latexrender/pictures/da2cc09fd363467cf6535b4fde596ec3.png)
![y_2=(c-\sqrt[]{\Delta})/2a... y_2=(c-\sqrt[]{\Delta})/2a...](/latexrender/pictures/d644017f4a1b6b8f010fd6a125fd000c.png)


 .
.
 :
: