-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480007 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 537866 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501613 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 722571 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2156160 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por zenildo » Ter Mai 31, 2016 09:50
por zenildo » Ter Mai 31, 2016 09:50
Essa questão tentei fazer por Pitágoras e depois fiz algumas manipulaçoes com a relação fundamental. Contudo, não deu nada certo. Poderia esclarecer como devo fazer?
- Anexos
-

-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Ana Cotrim » Qui Jun 02, 2016 05:50
por Ana Cotrim » Qui Jun 02, 2016 05:50
Acho que e bom fazeres um esboco do grafico que te e dado ai como por exemplo desenhar o criculo trigonometrico e nesse caso destacar o 1 quadrante. E de reparar tambem que nessa regiao pede cos<1/5 logo (caso consiga usar calculadora) faca cos^-1(que se encontra na calculadora como uma tecla secundaria) e veja o valor em graus (de lembrar que neste caso a calculadora tem de estar em "deg") e pintar o grafico nessa zona. Assim consegue ver em que zona o teta se encontra e assim consegue resolver o exercicio.
Outra alternativa se conseguir vizualizar e so meter o cos^-1 na calculadora ver o valor e responder.
Espero ter sido esclarecedora.
Neste caso a mim esta a dar-me um angulo de 78 graus logo o teta esta entre 75 e 90.
-
Ana Cotrim
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jun 02, 2016 05:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Quimica
- Andamento: cursando
 por adauto martins » Qui Jun 02, 2016 19:22
por adauto martins » Qui Jun 02, 2016 19:22
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Jun 03, 2016 11:55
por adauto martins » Sex Jun 03, 2016 11:55
uma correçao:
a funçao arcosseno no intervalo
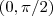
é decrescente,logo:
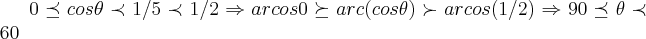
...temos q.
![{sen\theta}^{2}+{(1/5)}^{2}=1\Rightarrow sen\theta=2.\sqrt[]{6}/5\simeq 0.98\succ 0.96 =sen(75)\Rightarrow sen\theta \succ sen75\Rightarrow arcsen\theta\prec arcsen75\Rightarrow \theta\prec75 {sen\theta}^{2}+{(1/5)}^{2}=1\Rightarrow sen\theta=2.\sqrt[]{6}/5\simeq 0.98\succ 0.96 =sen(75)\Rightarrow sen\theta \succ sen75\Rightarrow arcsen\theta\prec arcsen75\Rightarrow \theta\prec75](/latexrender/pictures/4c0441b3ce578ed9024b03ceb1392df3.png)
,logo resolvendo as inequaçoes teremos:
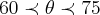
...
ps-aqui usei os valores de sen75,q. pode ser calculado usando pitagoras,pra encurtar o caminho usei os valores calculados...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por DanielFerreira » Sáb Jun 04, 2016 23:37
por DanielFerreira » Sáb Jun 04, 2016 23:37
Fazendo uso da calculadora, temos que
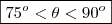
. Pois,
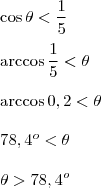
Ana, repare que
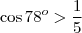
. Portanto, o ângulo não pode ser 78º.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Pelo Amor de Deus Ajuda
por jean » Ter Nov 25, 2008 18:51
- 2 Respostas
- 2524 Exibições
- Última mensagem por jean

Ter Nov 25, 2008 21:42
Pedidos
-
- [física] Ajuda Pelo amor d Deus
 por thialarcon1 » Sex Jun 13, 2008 13:59
por thialarcon1 » Sex Jun 13, 2008 13:59
- 4 Respostas
- 4733 Exibições
- Última mensagem por Neperiano

Seg Jun 18, 2012 18:11
Dúvidas Pendentes (aguardando novos colaboradores)
-
- Função do 1°grau Pelo amor de Deus ajuda ai!
por matheusfelipe » Sáb Jul 14, 2012 00:01
- 2 Respostas
- 2526 Exibições
- Última mensagem por matheusfelipe

Sáb Jul 14, 2012 00:48
Funções
-
- Ajuda aqui!
por Liahtz » Sex Ago 07, 2015 17:38
- 1 Respostas
- 9117 Exibições
- Última mensagem por nakagumahissao

Sáb Ago 08, 2015 11:33
Matrizes e Determinantes
-
- ajuda aqui!
 por zenildo » Seg Mai 09, 2016 01:18
por zenildo » Seg Mai 09, 2016 01:18
- 5 Respostas
- 8626 Exibições
- Última mensagem por zenildo

Qui Mai 12, 2016 22:41
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





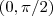 é decrescente,logo:
é decrescente,logo: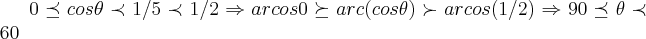 ...temos q.
...temos q. ![{sen\theta}^{2}+{(1/5)}^{2}=1\Rightarrow sen\theta=2.\sqrt[]{6}/5\simeq 0.98\succ 0.96 =sen(75)\Rightarrow sen\theta \succ sen75\Rightarrow arcsen\theta\prec arcsen75\Rightarrow \theta\prec75 {sen\theta}^{2}+{(1/5)}^{2}=1\Rightarrow sen\theta=2.\sqrt[]{6}/5\simeq 0.98\succ 0.96 =sen(75)\Rightarrow sen\theta \succ sen75\Rightarrow arcsen\theta\prec arcsen75\Rightarrow \theta\prec75](/latexrender/pictures/4c0441b3ce578ed9024b03ceb1392df3.png) ,logo resolvendo as inequaçoes teremos:
,logo resolvendo as inequaçoes teremos: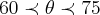 ...
...
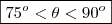 . Pois,
. Pois,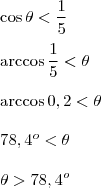
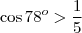 . Portanto, o ângulo não pode ser 78º.
. Portanto, o ângulo não pode ser 78º.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.