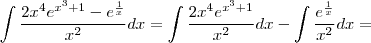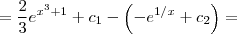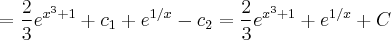-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478649 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534360 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 497938 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 713065 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2134433 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Douglas13 » Qua Nov 25, 2015 10:49
por Douglas13 » Qua Nov 25, 2015 10:49
Gostaria de saber se alguém poderia me ajudar a resolver essa
integral
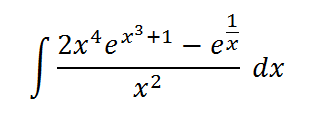
- unnamed.png (2.39 KiB) Exibido 5104 vezes
De preferência passo a passo para que possa compreender.
-
Douglas13
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Nov 25, 2015 10:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por nakagumahissao » Qua Nov 25, 2015 13:45
por nakagumahissao » Qua Nov 25, 2015 13:45
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por nakagumahissao » Qua Nov 25, 2015 13:48
por nakagumahissao » Qua Nov 25, 2015 13:48
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Douglas13 » Qua Nov 25, 2015 21:13
por Douglas13 » Qua Nov 25, 2015 21:13
Nakagumahissao Muito obrigado pela ajuda, não consegui resolver essa integral
-
Douglas13
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Nov 25, 2015 10:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição / Integral por partes
por Carlos28 » Seg Out 19, 2015 12:25
- 1 Respostas
- 2700 Exibições
- Última mensagem por nakagumahissao

Seg Out 19, 2015 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição
por Aliocha Karamazov » Qui Fev 23, 2012 23:57
- 2 Respostas
- 1978 Exibições
- Última mensagem por MarceloFantini

Sex Fev 24, 2012 12:07
Cálculo: Limites, Derivadas e Integrais
-
- Integral (substituição)
por kika_sanches » Sex Mar 23, 2012 14:42
- 4 Respostas
- 2651 Exibições
- Última mensagem por kika_sanches

Sex Mar 23, 2012 15:35
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Dom Nov 18, 2012 10:46
- 1 Respostas
- 1546 Exibições
- Última mensagem por young_jedi

Dom Nov 18, 2012 10:54
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao (u.du)
por menino de ouro » Seg Nov 19, 2012 16:23
- 7 Respostas
- 3865 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 21:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



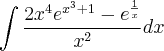
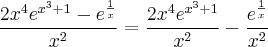
![\int \frac{2x^{4} e^{x^3 + 1}}{x^{2}} dx - \int \frac{e^{\frac{1}{x}}}{x^{2}} dx \;\;\;\;[1] \int \frac{2x^{4} e^{x^3 + 1}}{x^{2}} dx - \int \frac{e^{\frac{1}{x}}}{x^{2}} dx \;\;\;\;[1]](/latexrender/pictures/de5b2b7432b7867dd8e02e375194d4fa.png)
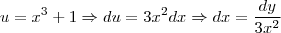
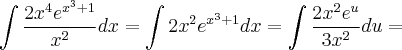
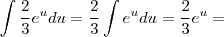
![= \frac{2}{3} e^{x^{3} + 1} + c_{1} \;\;\;\;\;[2] = \frac{2}{3} e^{x^{3} + 1} + c_{1} \;\;\;\;\;[2]](/latexrender/pictures/115b083fef63440a4025c93e971fccfc.png)
![u = \frac{1}{x} \;\;\;\; [3] u = \frac{1}{x} \;\;\;\; [3]](/latexrender/pictures/eb18e68730dac2bbad3d8f70b5395bb6.png)
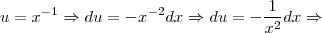
![\Rightarrow dx = - x^{2} du \;\;\;[4] \Rightarrow dx = - x^{2} du \;\;\;[4]](/latexrender/pictures/d0c2a27225bd8189267ea89f7d750b5c.png)
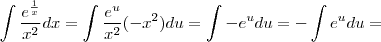
![= -e^{u} + c_{2} = -e^{1/x} + c_{2} \;\;\;\;\;[5] = -e^{u} + c_{2} = -e^{1/x} + c_{2} \;\;\;\;\;[5]](/latexrender/pictures/beae4a65e8797307c8b6edf98f394783.png)
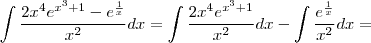
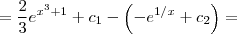
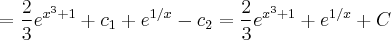


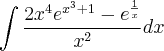
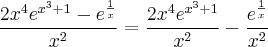
![\int \frac{2x^{4} e^{x^3 + 1}}{x^{2}} dx - \int \frac{e^{\frac{1}{x}}}{x^{2}} dx \;\;\;\;[1] \int \frac{2x^{4} e^{x^3 + 1}}{x^{2}} dx - \int \frac{e^{\frac{1}{x}}}{x^{2}} dx \;\;\;\;[1]](/latexrender/pictures/de5b2b7432b7867dd8e02e375194d4fa.png)
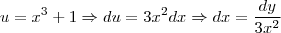
![= \frac{2}{3} e^{x^{3} + 1} + c_{1} \;\;\;\;\;[2] = \frac{2}{3} e^{x^{3} + 1} + c_{1} \;\;\;\;\;[2]](/latexrender/pictures/115b083fef63440a4025c93e971fccfc.png)
![u = \frac{1}{x} \;\;\;\; [3] u = \frac{1}{x} \;\;\;\; [3]](/latexrender/pictures/eb18e68730dac2bbad3d8f70b5395bb6.png)
![\Rightarrow dx = - x^{2} du \;\;\;[4] \Rightarrow dx = - x^{2} du \;\;\;[4]](/latexrender/pictures/d0c2a27225bd8189267ea89f7d750b5c.png)
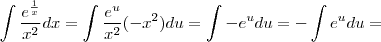
![= -e^{u} + c_{2} = -e^{1/x} + c_{2} \;\;\;\;\;[5] = -e^{u} + c_{2} = -e^{1/x} + c_{2} \;\;\;\;\;[5]](/latexrender/pictures/beae4a65e8797307c8b6edf98f394783.png)