 por Fontelles » Qua Dez 23, 2009 22:02
por Fontelles » Qua Dez 23, 2009 22:02
Fiquei em dúvida nessa questão.
2sen²x + |senx| - 1 = 0
Não era só eu trabalhar |senx| = senx, se senx > 0 ou |senx| = -senx, se senx < 0
E então ficaria:
2sen²x + senx -1 = 0 e outra equação 2sen²x - senx - 1 = 0
Descubro a solução em cada uma e será essa a resposta final?
-
Fontelles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Dez 09, 2009 01:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fontelles » Qua Dez 23, 2009 22:05
por Fontelles » Qua Dez 23, 2009 22:05
No caso encontro senx = - 1 ou senx = 1/2 ou senx = 1 ou senx = -1/2
Esqueci de dizer que segue o intervalo [0, 2pi]
Sei que não bate com os valores de senx = -1 e senx = 1, mas queria saber o meu erro na procedência.
-
Fontelles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Dez 09, 2009 01:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Dez 24, 2009 04:18
por MarceloFantini » Qui Dez 24, 2009 04:18
Equação original:
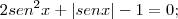
Portanto, para
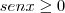
, temos:
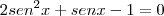
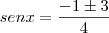
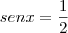
ou
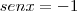
(Não convém, pois
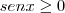
).
Para
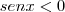
, temos:
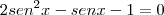
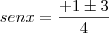
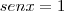
(Não convém, pois
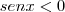
) ou

.
Espero que tenha entendido.
Feliz Natal, e um abraço!
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fontelles » Dom Dez 27, 2009 08:55
por Fontelles » Dom Dez 27, 2009 08:55
Poxa, esqueci dessa parte da propriedade.
Muito obrigado, Fantini!
Felicidades!
-
Fontelles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qua Dez 09, 2009 01:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3594 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- Módulo
por Rodrigo Tomaz » Sex Fev 19, 2010 11:36
- 4 Respostas
- 3018 Exibições
- Última mensagem por MarceloFantini

Sex Mar 05, 2010 16:09
Funções
-
- Modulo
por Sandy26 » Ter Abr 27, 2010 14:46
- 5 Respostas
- 3006 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 17:57
Álgebra Elementar
-
- Módulo
por Bebel » Dom Ago 08, 2010 00:24
- 0 Respostas
- 1380 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:24
Números Complexos
-
- Modulo.
por 380625 » Qui Mar 17, 2011 11:21
- 2 Respostas
- 2096 Exibições
- Última mensagem por LuizAquino

Sex Set 09, 2011 10:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


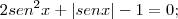
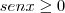 , temos:
, temos: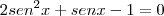

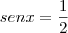 ou
ou 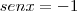 (Não convém, pois
(Não convém, pois 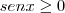 ).
).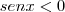 , temos:
, temos: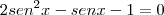

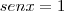 (Não convém, pois
(Não convém, pois  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.