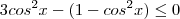-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477756 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 528765 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492302 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 696932 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2105881 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Rafael16 » Qui Mai 23, 2013 21:28
por Rafael16 » Qui Mai 23, 2013 21:28
Boa noite!
Resolva, no intervalo
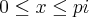
, a inequação
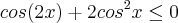
.
Tentei resolver da seguinte maneira (que nem sei se estou no caminho certo

):
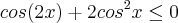
Transformei cos(2x) em produto:
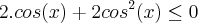
![2.cos(x) . [1 + cos(x)] \leq 0 2.cos(x) . [1 + cos(x)] \leq 0](/latexrender/pictures/f36f3bd9d0d22064894b2486b3613700.png)
Cheguei nessa inequação produto, e tentei fazer o procedimento igual numa inequação produto comum (transformar cada fator em função, achar as raízes e '"jogar" as raízes na reta pra fazer o jogo de sinais)
A raíz de 2cos(x)=0 é x=pi/2 e a raíz de 1 + cos(x) = 0 é x= pi
Mas na hora de colocar na reta me confundi.
Como que faço esse trem?

Resposta:

{
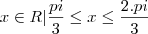
}
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Molina » Qui Mai 23, 2013 21:55
por Molina » Qui Mai 23, 2013 21:55
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Rafael16 » Qui Mai 23, 2013 23:07
por Rafael16 » Qui Mai 23, 2013 23:07
Valeu
Molina!
Então
![tg(x)\geq \sqrt[]{3} tg(x)\geq \sqrt[]{3}](/latexrender/pictures/6ccd31622e44e5215b22317b513a5165.png)
tem como solução
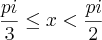
ou

.
Então a resposta esta errada, né?
Molina escreveu:Não entendi muito bem essa sua transformação, pois

.
Fiz assim:



Esta certo assim também?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Molina » Qui Mai 23, 2013 23:20
por Molina » Qui Mai 23, 2013 23:20
Boa noite.
Vou tentar resolver sem utilizar tangente, pois em

ela não está definida, como você salientou. Mas observe que este ponto é uma solução da inequação. Volto a fazer contato em breve.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Qui Mai 23, 2013 23:31
por Molina » Qui Mai 23, 2013 23:31
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Rafael16 » Sex Mai 24, 2013 00:16
por Rafael16 » Sex Mai 24, 2013 00:16
Obrigado Molina!
Então a forma que você resolveu na primeira resolução (com tangente) esta errada?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por Molina » Sex Mai 24, 2013 00:20
por Molina » Sex Mai 24, 2013 00:20
Rafael16 escreveu:Obrigado Molina!
Então a forma que você resolveu na primeira resolução (com tangente) esta errada?
Está sim, pois eu passei o cosseno dividindo e ele poderia ser 0, o que não pode na matemática.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequação trigonométrica
por manuoliveira » Dom Jun 20, 2010 14:23
- 1 Respostas
- 1478 Exibições
- Última mensagem por Douglasm

Dom Jun 20, 2010 16:09
Trigonometria
-
- Inequação trigonométrica
por Capelett » Sex Jun 17, 2011 15:41
- 0 Respostas
- 1096 Exibições
- Última mensagem por Capelett

Sex Jun 17, 2011 15:41
Trigonometria
-
- Inequação trigonometrica
por tigre matematico » Qua Out 19, 2011 20:03
- 0 Respostas
- 1107 Exibições
- Última mensagem por tigre matematico

Qua Out 19, 2011 20:03
Trigonometria
-
- Inequação trigonométrica
por crsjcarlos » Qua Dez 05, 2012 17:36
- 1 Respostas
- 1585 Exibições
- Última mensagem por e8group

Qua Dez 05, 2012 21:36
Trigonometria
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 5436 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
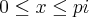 , a inequação
, a inequação 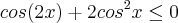 .
. ):
):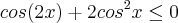
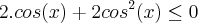
![2.cos(x) . [1 + cos(x)] \leq 0 2.cos(x) . [1 + cos(x)] \leq 0](/latexrender/pictures/f36f3bd9d0d22064894b2486b3613700.png)

 {
{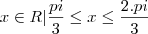 }
}

 . Assim:
. Assim: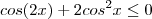
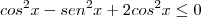

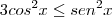

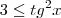


![tg(x)\geq \sqrt[]{3} tg(x)\geq \sqrt[]{3}](/latexrender/pictures/6ccd31622e44e5215b22317b513a5165.png) tem como solução
tem como solução 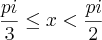 ou
ou  .
.


 ela não está definida, como você salientou. Mas observe que este ponto é uma solução da inequação. Volto a fazer contato em breve.
ela não está definida, como você salientou. Mas observe que este ponto é uma solução da inequação. Volto a fazer contato em breve.