 por yanagranhen » Qua Jun 23, 2010 22:37
por yanagranhen » Qua Jun 23, 2010 22:37
Simplifique
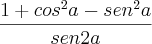
a) -1
b) tg a
c) cotg ad) cossec a
e) sec a
Já tentei utilizar todas as relações trigonométricas, no final sobra como resposta cossec 2a + cotg 2a e não sei o que fazer daí em diante!
Me ajudem!
-
yanagranhen
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jun 17, 2010 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia florestal
- Andamento: cursando
 por Lucio Carvalho » Qua Jun 23, 2010 23:03
por Lucio Carvalho » Qua Jun 23, 2010 23:03
Olá yanagranhen,
Apresento a seguinte ajuda:
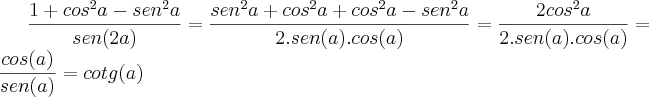
Espero ter ajudado!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por yanagranhen » Qua Jun 23, 2010 23:20
por yanagranhen » Qua Jun 23, 2010 23:20
Mas
sen²a + cos²a = 1
cos²a = 1 - sen²a
ou
sen²a = 1 - cos²a
e como você substituiu 1 + cos²a por sen²a?
-
yanagranhen
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jun 17, 2010 00:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia florestal
- Andamento: cursando
 por MarceloFantini » Qui Jun 24, 2010 08:18
por MarceloFantini » Qui Jun 24, 2010 08:18
Ele não substituiu
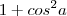
por
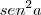
. Ele substituiu

por

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações
por Rose » Qui Mai 15, 2008 14:41
- 1 Respostas
- 1957 Exibições
- Última mensagem por admin

Qui Mai 15, 2008 16:38
Funções
-
- Relações
por chronoss » Seg Mai 20, 2013 14:19
- 0 Respostas
- 1043 Exibições
- Última mensagem por chronoss

Seg Mai 20, 2013 14:19
Álgebra Elementar
-
- Relações
por livia02 » Qua Set 04, 2013 17:15
- 0 Respostas
- 1118 Exibições
- Última mensagem por livia02

Qua Set 04, 2013 17:15
Álgebra Elementar
-
- [Relações]
por Giudav » Ter Fev 11, 2014 18:38
- 1 Respostas
- 2554 Exibições
- Última mensagem por DanielFerreira

Qua Fev 12, 2014 17:47
Sequências
-
- Relações no círculo
por RBenicio » Qua Set 16, 2009 15:34
- 3 Respostas
- 2822 Exibições
- Última mensagem por Molina

Qui Set 17, 2009 14:45
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
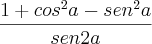

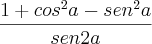

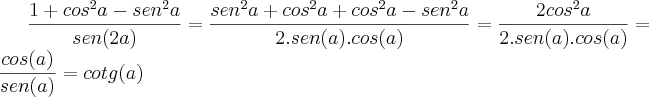




 .
.



