 por mota_16 » Qua Dez 11, 2013 20:12
por mota_16 » Qua Dez 11, 2013 20:12
Pessoal, esse eu não consegui fazer. Tentei substituir o
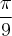
na euqação, mas sem sucesso. Passei a resolver as equações do enunciado, mas não soube o que fazer com as suas raízes.
Pode-se mostrar que
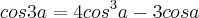
. Uma decorrência dessa fórmula é que
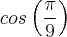
é solução da equação:
a)
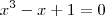
b)
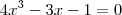
c)
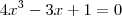
d)
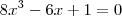
e)
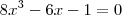
Gabarito: E
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 20:38
por e8group » Qua Dez 11, 2013 20:38
Sai de imediato da relação dada com escolha particular para

.Aceitando que
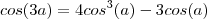
. Segue-se que
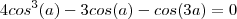
. Em particular para
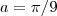
obterá o resultado .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Qua Dez 11, 2013 20:48
por mota_16 » Qua Dez 11, 2013 20:48
Desculpe-me a falta de conhecimento.
De fato, tinha feito isso mesmo:
Escrevi
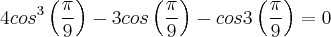
. Mas aqui eu parei, pois
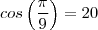
graus e não é um ângulo notável.
Como prosseguir?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 20:58
por e8group » Qua Dez 11, 2013 20:58
Não se preocupe ,o objetivo não é calcular o cosseno de
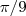
,como tu notou não é notável . Só queremos saber quais das alternativas apresentam a equação cuja solução é
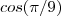
. Tente novamente e caso não consiga post .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Qua Dez 11, 2013 21:09
por mota_16 » Qua Dez 11, 2013 21:09
Minha dúvida é a seguinte: eu não sei o valor de cos(pi/9), mas preciso identificar qual a equação das alternativas tem esse valor. Aqui já me deu um nó. E outra as equações das alternativas não são trigonométricas, então como eu vou saber qual delas é a correta?
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 21:13
por e8group » Qua Dez 11, 2013 21:13
Veja um exemplo para exemplificar :
Sabendo-se que para certo

(complexo) tem-se
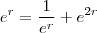
. Segue daí ,
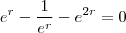
e multiplicando por
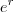
,
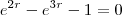
ou ainda
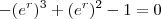
. E aqui vemos que
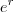
corresponde a uma das soluções da eq. polinomial
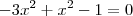
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 21:20
por e8group » Qua Dez 11, 2013 21:20
Não precisa veric
mota_16 escreveu:Minha dúvida é a seguinte: eu não sei o valor de cos(pi/9), mas preciso identificar qual a equação das alternativas tem esse valor. Aqui já me deu um nó. E outra as equações das alternativas não são trigonométricas, então como eu vou saber qual delas é a correta?
Veja outro exemplo simples só para ver se você compreendeu .
Suponha-se que

para certo

(Não precisar calcular ) . Me diga uma equação polinomial de grau 2 em que

é solução .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por mota_16 » Qua Dez 11, 2013 23:26
por mota_16 » Qua Dez 11, 2013 23:26
Agora sim, acho que compreendi.
Pensei em fazer assim:
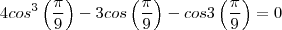
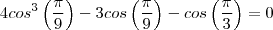
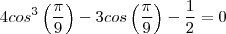
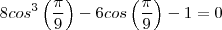
É isso, não é?
Nada como um bom professor. Muito obrigado santhiago!
-
mota_16
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Dez 06, 2013 10:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Regular
- Andamento: cursando
 por e8group » Qua Dez 11, 2013 23:30
por e8group » Qua Dez 11, 2013 23:30
Não há de quê . É isso ,está correto,conseguiu chegar lá !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7731 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13236 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13024 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8712 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
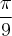 na euqação, mas sem sucesso. Passei a resolver as equações do enunciado, mas não soube o que fazer com as suas raízes.
na euqação, mas sem sucesso. Passei a resolver as equações do enunciado, mas não soube o que fazer com as suas raízes.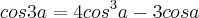 . Uma decorrência dessa fórmula é que
. Uma decorrência dessa fórmula é que 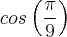 é solução da equação:
é solução da equação: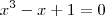
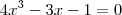
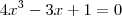
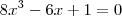
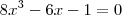

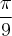 na euqação, mas sem sucesso. Passei a resolver as equações do enunciado, mas não soube o que fazer com as suas raízes.
na euqação, mas sem sucesso. Passei a resolver as equações do enunciado, mas não soube o que fazer com as suas raízes.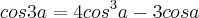 . Uma decorrência dessa fórmula é que
. Uma decorrência dessa fórmula é que 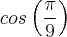 é solução da equação:
é solução da equação: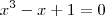
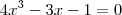
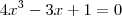
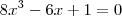
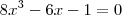

 .Aceitando que
.Aceitando que 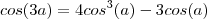 . Segue-se que
. Segue-se que 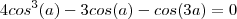 . Em particular para
. Em particular para 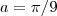 obterá o resultado .
obterá o resultado .
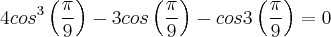 . Mas aqui eu parei, pois
. Mas aqui eu parei, pois 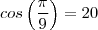 graus e não é um ângulo notável.
graus e não é um ângulo notável.
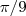 ,como tu notou não é notável . Só queremos saber quais das alternativas apresentam a equação cuja solução é
,como tu notou não é notável . Só queremos saber quais das alternativas apresentam a equação cuja solução é 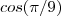 . Tente novamente e caso não consiga post .
. Tente novamente e caso não consiga post .

 (complexo) tem-se
(complexo) tem-se 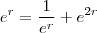 . Segue daí ,
. Segue daí ,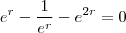 e multiplicando por
e multiplicando por 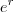 ,
, 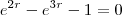 ou ainda
ou ainda 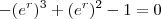 . E aqui vemos que
. E aqui vemos que 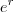 corresponde a uma das soluções da eq. polinomial
corresponde a uma das soluções da eq. polinomial 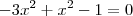 .
.
 para certo
para certo  (Não precisar calcular ) . Me diga uma equação polinomial de grau 2 em que
(Não precisar calcular ) . Me diga uma equação polinomial de grau 2 em que  é solução .
é solução .
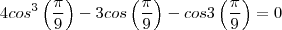
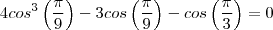
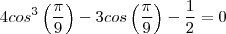
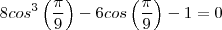




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.