 por Rafael16 » Ter Jul 23, 2013 17:51
por Rafael16 » Ter Jul 23, 2013 17:51
Resolvi a equação da seguinte maneira:





Daí cheguei na seguinte solução:
S = {x e R| x = pi/2 + k.pi ou x = pi/8 + k.pi/4, k e Z}
Enfim, gostaria de saber se tem uma outra forma de resolver essa equação.
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por MateusL » Qua Jul 24, 2013 15:46
por MateusL » Qua Jul 24, 2013 15:46
Olá!
Acredito que essa seja uma das formas mais simples de resolver.
Todas as outras formas que consegui pensar não são tão simples como essa.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Rafael16 » Qua Jul 24, 2013 16:15
por Rafael16 » Qua Jul 24, 2013 16:15
MateusL escreveu:Olá!
Acredito que essa seja uma das formas mais simples de resolver.
Todas as outras formas que consegui pensar não são tão simples como essa.
Abraço!
Obrigado
MateusL!
Estava pensando dessa maneira:
cos(a) = cos(b) --> a = b + 2k.pi ou a = - b + 2k.pi
Só que dessa maneira não iria da certo por causa do sinal negativo (cos 5x = - cos 3x). Certo?

-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por MateusL » Qui Jul 25, 2013 17:51
por MateusL » Qui Jul 25, 2013 17:51
Rafael16 escreveu:Obrigado
MateusL!
Estava pensando dessa maneira:
cos(a) = cos(b) --> a = b + 2k.pi ou a = - b + 2k.pi
Só que dessa maneira não iria da certo por causa do sinal negativo (cos 5x = - cos 3x). Certo?

Errado! Daria certo! Tu só terias que notar que
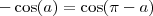
, então obterías

. Até cheguei a pensar em algo do tipo, mas, à primeira vista, me pareceu que daria mais trabalho, mas realmente fica mais simples:


Note que

, apesar de estar escrito de maneira diferente, é uma solução equivalente a

.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cosseno
por karen » Ter Nov 27, 2012 13:17
- 1 Respostas
- 1562 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 19:24
Trigonometria
-
- Cosseno (FUVEST)
 por Ananda » Sex Mar 14, 2008 22:37
por Ananda » Sex Mar 14, 2008 22:37
- 4 Respostas
- 6404 Exibições
- Última mensagem por Ananda

Seg Mar 17, 2008 17:28
Geometria Espacial
-
- Função Cosseno
por DanielFerreira » Qui Jul 30, 2009 17:41
- 1 Respostas
- 2870 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:01
Trigonometria
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4659 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 18809 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.















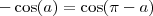 , então obterías
, então obterías  . Até cheguei a pensar em algo do tipo, mas, à primeira vista, me pareceu que daria mais trabalho, mas realmente fica mais simples:
. Até cheguei a pensar em algo do tipo, mas, à primeira vista, me pareceu que daria mais trabalho, mas realmente fica mais simples:

 , apesar de estar escrito de maneira diferente, é uma solução equivalente a
, apesar de estar escrito de maneira diferente, é uma solução equivalente a  .
.