 por rodsales » Dom Nov 15, 2009 18:45
por rodsales » Dom Nov 15, 2009 18:45
Dois lados de um triângulo medem 6m e 10m e formam entre si um ângulo de 120º. Determine a medida do terceiro lado.
O que eu gostaria de saber quando vou calcular um exercício desse estilo se terei que usar a lei dos senos ou dos cossenos? E por quê?
obs: esse exercício é bem simples, mas sempre fico na dúvida em qual usar.
Grato.
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Lucio Carvalho » Seg Nov 16, 2009 10:56
por Lucio Carvalho » Seg Nov 16, 2009 10:56
Olá rodsales,
Tentarei ajudar.
Como bem sabes, para qualquer triângulo são conhecidas as fórmulas:
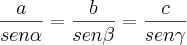
(teorema dos senos)
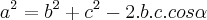
(teorema dos co-senos)
Estas relações permitem resolver triângulos, isto é, conhecidos alguns dos seus elementos podem determinar-se os outros.
De acordo com o teu exercício, temos os comprimentos de dois lados e o ângulo por eles formado. Assim, vamos utilizar o teorema dos co-senos.
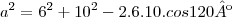
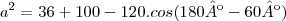
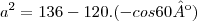
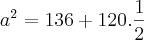
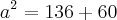
![a=\sqrt[]{196} a=\sqrt[]{196}](/latexrender/pictures/ba58d9aa46e5afa5f7883ea9c3901630.png)

Nota: Quando sabemos, por exemplo, as medidas de dois lados de triângulo e o ângulo oposto a um deles, podemos utilizar o teorema dos senos.
Espero ter ajudado e até breve!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Área de triângulos quaisquer
por -Sarah- » Seg Ago 19, 2013 20:32
- 6 Respostas
- 4008 Exibições
- Última mensagem por young_jedi

Ter Ago 20, 2013 23:48
Trigonometria
-
- (Fuvest) Relações Métricas em Triângulos Quaisquer - Ajudem!
 por kamillanjb » Sex Jul 22, 2011 15:00
por kamillanjb » Sex Jul 22, 2011 15:00
- 1 Respostas
- 6993 Exibições
- Última mensagem por FilipeCaceres

Sex Jul 22, 2011 21:18
Geometria Plana
-
- Resolução de Triângulos - Questão
por rvitorper » Sex Mar 25, 2011 00:05
- 0 Respostas
- 1175 Exibições
- Última mensagem por rvitorper

Sex Mar 25, 2011 00:05
Trigonometria
-
- [Semelhança de triângulos] Triângulos quadrados
 por Debora Bruna » Seg Ago 08, 2016 12:18
por Debora Bruna » Seg Ago 08, 2016 12:18
- 0 Respostas
- 1476 Exibições
- Última mensagem por Debora Bruna

Seg Ago 08, 2016 12:18
Geometria Plana
-
- Triângulos
por claudia » Ter Nov 11, 2008 13:58
- 14 Respostas
- 10893 Exibições
- Última mensagem por claudia

Ter Nov 18, 2008 14:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


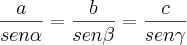 (teorema dos senos)
(teorema dos senos)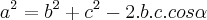 (teorema dos co-senos)
(teorema dos co-senos)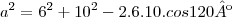
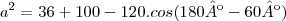
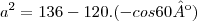
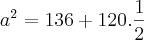
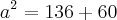
![a=\sqrt[]{196} a=\sqrt[]{196}](/latexrender/pictures/ba58d9aa46e5afa5f7883ea9c3901630.png)

