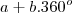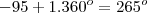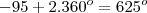por Maria Livia » Sáb Out 13, 2012 08:30
Determine os arcos positivos, menores que 2000 graus, côngruos de -95 graus?
-
Maria Livia
- Usuário Parceiro
-
- Mensagens: 79
- Registrado em: Seg Ago 13, 2012 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por Maria Livia » Sáb Out 13, 2012 08:36
Eu só consegui achar a primeira determinação positiva : 2000/360= 5 com resto de 200, portanto 200 seria a primeira determinação positiva mas e depois?
-
Maria Livia
- Usuário Parceiro
-
- Mensagens: 79
- Registrado em: Seg Ago 13, 2012 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por Maria Livia » Sex Out 19, 2012 17:40
Alguém me ajuda pf?
-
Maria Livia
- Usuário Parceiro
-
- Mensagens: 79
- Registrado em: Seg Ago 13, 2012 13:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por young_jedi » Sex Out 19, 2012 18:36
veja que qualquer angulo pode ser escrito como
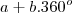
então vamos fazer
para b=1
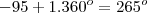
então 265º é congruo a -95º
agora para b=2
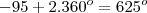
então 625º é congruo a -95º
agora tente determinar todos que são menores que 2000º
-
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinação Geral de Arcos Côngruos
por danielcp » Sex Dez 26, 2014 17:46
- 1 Respostas
- 1610 Exibições
- Última mensagem por Russman
Sex Dez 26, 2014 23:19
Trigonometria
-
- Arcos congruos
por Maria Livia » Sáb Out 13, 2012 08:22
- 1 Respostas
- 3649 Exibições
- Última mensagem por young_jedi
Sáb Out 13, 2012 11:36
Trigonometria
-
- vetor ortonormal positiva
por Ana Maria da Silva » Seg Abr 08, 2013 15:46
- 1 Respostas
- 912 Exibições
- Última mensagem por e8group
Seg Abr 08, 2013 16:15
Geometria Analítica
-
- Direção positiva em reta decrescente
por eric976 » Seg Out 05, 2009 16:05
- 2 Respostas
- 1823 Exibições
- Última mensagem por eric976
Qua Out 07, 2009 11:01
Trigonometria
-
- (UNICAMP) Raíz real positiva
por Carolziiinhaaah » Sex Fev 04, 2011 15:32
- 0 Respostas
- 1141 Exibições
- Última mensagem por Carolziiinhaaah
Sex Fev 04, 2011 15:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
