 por Alerecife » Sáb Set 08, 2012 13:32
por Alerecife » Sáb Set 08, 2012 13:32
Como posso demostra:
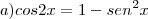

c) E resolver
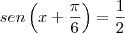
em
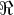
d) E resolver no intervalo
![\left[0,2\pi \right] \left[0,2\pi \right]](/latexrender/pictures/bba974a4663c6b343b265fc813462924.png)
a inequação
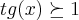
pela atenção obrigado!
-
Alerecife
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Set 04, 2012 12:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: cursando
 por Alerecife » Dom Set 09, 2012 13:46
por Alerecife » Dom Set 09, 2012 13:46
Ok vamos lá vejam ate aonde eu cheguei:
a)

minha duvida:

Na letra b) eu cheguei ate

a letra e c) o método de resposta é semelhante?
pela atenção obrigado!
-
Alerecife
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Set 04, 2012 12:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: cursando
 por young_jedi » Dom Set 09, 2012 16:36
por young_jedi » Dom Set 09, 2012 16:36
Na letra a) acho que seu raciocinio esta correto consulte a questão
Na letra b) temos que

usando as identidades trigonometricas temos


sendo assim temos

Na letra c) podemos perceber que os angulos que tem seu seno como sendo igual a meio são os angulos

e

sendo assim temos que para x satisfazer a equação deve ser igual a

ou

onde

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por MarceloFantini » Dom Set 09, 2012 17:45
por MarceloFantini » Dom Set 09, 2012 17:45
Na letra (a) o correto deve ser

. Você está no caminho correto. Para a letra (b), note que




.
Na letra (c), como ele quer que resolvamos para
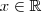
, devemos fazer

e

, pois não é possível escrever tudo como um conjunto só. Daí, teremos que a solução é o conjunto

.
Por último, teremos que

se

ou

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Identidades Trigonométricas
por ElizabethS2 » Dom Nov 21, 2010 18:54
- 7 Respostas
- 3632 Exibições
- Última mensagem por caroltoscaON

Qua Nov 24, 2010 18:51
Trigonometria
-
- Identidades Trigonométricas
por Camila Z » Seg Jan 16, 2012 23:15
- 17 Respostas
- 9870 Exibições
- Última mensagem por Camila Z

Qui Jan 19, 2012 19:25
Trigonometria
-
- INTEGRAIS UTILIZANDO AS IDENTIDADES TRIGONOMETRICAS
por Fabiano28 » Seg Mar 23, 2015 17:32
- 0 Respostas
- 1634 Exibições
- Última mensagem por Fabiano28

Seg Mar 23, 2015 17:32
Cálculo: Limites, Derivadas e Integrais
-
- Demostração
por Balanar » Dom Ago 29, 2010 05:43
- 1 Respostas
- 954 Exibições
- Última mensagem por Douglasm

Dom Ago 29, 2010 15:56
Álgebra Elementar
-
- Demostração da Regra do Trapézio
por ARCS » Sex Fev 10, 2012 19:12
- 1 Respostas
- 1186 Exibições
- Última mensagem por LuizAquino

Sáb Fev 11, 2012 11:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
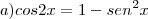

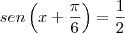 em
em 
![\left[0,2\pi \right] \left[0,2\pi \right]](/latexrender/pictures/bba974a4663c6b343b265fc813462924.png) a inequação
a inequação 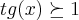

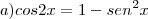

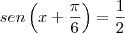 em
em 
![\left[0,2\pi \right] \left[0,2\pi \right]](/latexrender/pictures/bba974a4663c6b343b265fc813462924.png) a inequação
a inequação 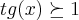









 e
e 
 ou
ou  onde
onde 

 . Você está no caminho correto. Para a letra (b), note que
. Você está no caminho correto. Para a letra (b), note que 


 .
.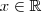 , devemos fazer
, devemos fazer  e
e  , pois não é possível escrever tudo como um conjunto só. Daí, teremos que a solução é o conjunto
, pois não é possível escrever tudo como um conjunto só. Daí, teremos que a solução é o conjunto .
. se
se  ou
ou  .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
